En dag blev det mest onyttiga nyttigt – kryptering, talteori och RSA
Tisdag 16 december 2003 kl 18.00-20.00
Clas Löfwall, clas
Johan Thorbiörnson, johan
| Matematiska
institutionen Avd matematik Stockholms universitet |
Matematisk
lusttur 5p Orienteringskurs Hösten 2003 www.math.su.se/lusttur/ |
Föreläsning
11
En dag blev det mest onyttiga nyttigt – kryptering,
talteori och RSA
Tisdag 16 december 2003 kl 18.00-20.00
Clas Löfwall,
clas![]() math.su.se
math.su.se
Johan Thorbiörnson,
johan![]() math.su.se
math.su.se
Inlämningsuppgift:
Någon skickar mig nu det kodade meddelandet 2. Vilket är det ursprungliga siffermeddelandet? |
Senaste
nytt (3 december 2003): |
Något
om RSA-algoritmen
(Texten
nedan är ett utdrag ur Förberedande kurs i matematik 5p,
avsnitt A12 Fördjupning, se http://www.math.su.se/forb/)
Detta fördjupningsavsnitt bygger på resultat om primtalsfaktorisering och något om räkning med rester, så kallad resträkning eller moduloräkning » (eller kongruensräkning), samt det resultat som kallas Fermats lilla sats ».
KRYPTERING
MED RSA
Det blir allt
viktigare att kunna sända information via Internet på ett säkert
sätt. Användningen av Internet till att sköta sina betalningar,
sända digitala signaturer och elektroniska dokument ökar alltmer.
Man kanske också inte har lust att alla ska kunna snoka och läsa
den epost man skickar till kompisar eller arbetskamrater.
|
Ett mycket vanligt program för kryptering är PGP
(Pretty Good Privacy) som också kan kallas för Internets rövarspråk.
Programmet bygger på världens idag mest kända krypteringsmetod
RSA (uppkallat efter upphovsmännen Ron Rivest, Adi Shamir
och Leonard Adelman som utvecklade algoritmen 1977). RSA är patentskyddat
i USA men får användas fritt av privatpersoner. Många av de
stora programvarujättarna använder RSA, t.ex. Microsoft, IBM, Adobe
och Apple. RSA används bland annat också för att säkra de elektroniska
nycklarna till den amerikanska kärnvapenarsenalen.
Teorin bakom RSA är relativt enkel och ger ett extremt säkert krypteringssystem.
Metoden bygger på att det är mycket lätt att multiplicera två
primtal men mycket krävande att faktorisera ett givet tal i sina primtalskomponenter
(om de ingående primtalen är stora). Det finns idag inga effektiva
metoder att faktorisera ett heltal i sina primtalskomponenter. Exempelvis är
7907 och 7919 två primtal och deras produkt beräknas lätt med
ett fåtal räkneoperationer till 62615533, men att faktorisera detta
tal skulle i princip kräva att man går igenom alla tänkbara
primtalsfaktorer upp till och med talet 7907. För en modern PC så
skulle det ta ca 5 år att faktorisera ett tal av storleken 10130
(d.v.s. ett tal med 130 siffror i 10-systemet).
Eftersom svårigheten att faktorisera ett tal växer
snabbt med storleken på talet blir det extremt värdefullt att hitta
metoder att faktorisera heltal som består av produkter av mycket stora
primtal. Idag kan man faktiskt bli rik om man hittar smarta sådana metoder.
Denna praktiska användning av primtal var det ingen som kunde förutse
fram till 1960-talet. Sedan antikens dagar hade primtalsforskning varit ett
exempel på något som totalt saknar praktisk tillämpning och
som endast hade inom-matematiskt intresse. Ett populärt skämt var
t.ex. att på dörren till fikarummet sätta upp en skylt med texten
"Institutionen för primtalsforskning". Idag skulle man vara en
mycket hipp och tidsmedveten person om man hade en sådan skylt till sitt
arbetsrum. Den som hittar nya sätt att attackera befintliga kryptosystem
blir snabbt mycket känd.
|
RSA-algoritmen är ett exempel på ett s.k. "public
key"-system, d.v.s. ett system med en offentlig nyckel, till
skillnad från system med en hemlig nyckel som både avsändaren
och mottagaren har utbytt i förväg och som bara de känner till.
En offentlig nyckel är en smart lösning som gör det möjligt för två personer
att skicka säkrade meddelanden emellan sig. Klassiska kryptosystem använder
en och samma nyckel för kryptering och dekryptering. Om man använder
ett sådant system så är problemet att hitta ett tillräckligt
säkert sätt att överföra nyckeln till det krypto man använder, men då
kunde man ju nästan lika gärna ha överfört meddelandet i sig. En offentlig nyckel
innebär att varje person har två nycklar: en hemlig som man inte lämnar
ut till någon och en offentlig som man lämnar ut överallt, t.ex. i slutet på
alla sina e-postmeddelanden. Den som vill kommunicera säkert med en person tar
denna persons offentliga nyckel som personen erbjuder offentligt, krypterar
med RSA-algoritmen meddelandet till personen med hjälp av den offentliga
nyckeln. Meddelandet kan nu bara dekrypteras med mottagarens hemliga nyckel
som bara denne känner till. Den offentliga nyckeln kan allstå användas
fritt av alla för att kryptera. Dekryptering kan endast ske med den hemliga
nyckeln.
Klartexten till meddelandena som krypteras är heltal, vilket inte
är någon inskränkning eftersom det är lätt att översätta
godtyckliga symboler och bilder till talföljder innan man sätter igång
och krypterar. Om vi vill sända ett textmeddelande med bokstäver ur
det svenska alfabetet så kan vi t.ex. komma överens om att varje
bokstav motsvaras av ett visst heltal. Man kan t.ex. låta bokstäverna
A, B, C, D... i alfabetet representeras av tvåsiffriga heltal 11, 12,
13, 14, etc:
| A | B | C | D | E | F | G | H | I | J | K | L | M | ... | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | ... |
I så fall skulle meddelandet
HEJ
representeras av heltalet
181519
Ett annat sätt är t.ex. att använda den vedertagna standarden ASCII (The American Standard Code for Information Interchange, uttalas på samma sätt som "ask-key" på engelska). Denna standard föreslogs 1963 och infördes slutligen 1968. Binärt använder man 7 stycken nollor och ettor, vilket ger talen från 0 till 127. Var och ett av dessa tal motsvarar ett tecken (bokstäver, siffror, interpunkteringstecken och specialtecken). The Extended ASCII Character Set bygger på 8 stycken ettor och nollor binärt och använder ytterligare 128 tal från 128 till 255 för att representera ytterligare matematiska och grafiska symboler samt diverse utländska bokstäver. I denna ASCII-kod representeras bokstäverna H, E, J av 072, 069 respektive 074.
|
M = meddelandet (en följd av siffror som vi uppfattar som ett heltal) N, k = offentliga nycklar (två heltal) C = krypterat meddelande, , se kommentaren till höger
d = hemlig nyckel, ett heltal som uppfyller 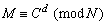
Vi visar först med två exempel hur algoritmen går till innan
vi förklarar teorin.
|
|
I faktiska exempel är de tal man använder som nycklar
betydligt större.
Hur fungerar RSA?
Vi ska nu förklara hur RSA fungerar. Algoritmen bygger på primtalsfaktorisering,
Eulers phi-funktion och ett klassiskt teorem som kallas "Fermats lilla
sats" (som är ett specialfall av "Eulers sats"). Algoritmen
är följande:
|
Att beräkna meddelandet i klartext
Vi har sett i punkt 1-6 ovan hur man tar fram sina offentliga nycklar (N och k) samt sin personliga nyckel d. Vi ska nu se hur man kan få tillbaka klartexten M från det krypterade meddelandet C via den hemliga nyckeln d genom att beräkna vilken rest Cd bildar vid division med N. Denna rest är klartexten M. Förklaringen ser man i följande kalkyl:
Vi använder
här att ![]() modulo
N, där N = pq. Detta följer ur följande resultat:
modulo
N, där N = pq. Detta följer ur följande resultat:
Fermats lilla sats:
För varje heltal a och varje primtal p gäller att ap — a är delbart med p.
(Läs om resultatet och dess bevis i A12 Fördjupning Fermats lilla sats » )
Hur ser man då
att ![]() modulo N följer från Fermats lilla sats? Låt oss göra
en kalkyl, men vi behöver först formulera om Fermats lilla sats till
följande form:
modulo N följer från Fermats lilla sats? Låt oss göra
en kalkyl, men vi behöver först formulera om Fermats lilla sats till
följande form:
Fermats lilla sats (alternativ formulering):
För varje primtal p och varje heltal a som inte är delbart med p gäller att ap — 1 — 1 är delbart med p.Detta kan också uttryckas
Vi kan nu med hjälp av detta resultat få
(*)
under förutsättning att M inte är delbart med p. På samma sätt, under förutsättning att M inte är delbart med q, så får vi
(**)
|
Om M uppfyller
förutsättningarna att varken vara delbart med p eller q,
så är alltså enligt (*) och (**) talet ![]() delbart med både p och q och således delbart med produkten
pq. Detta är samma sak som att
delbart med både p och q och således delbart med produkten
pq. Detta är samma sak som att
(mod pq )
vilket var det
vi behövde för att beräkna klartexten ovan
» och få ![]() .
Men detta gäller alltså bara under förutsättning att meddelandet
M varken är delbart med p eller q. Vi måste
också reda ut vad som gäller om M vore delbart med p eller
med q. Eftersom vi bara krypterar meddelanden M som är mindre
än pq så kan inte M vara delbart med både p
och q utan högst en av dem. Vi kan därför anta att
M är delbart med p, men ej med q. Fallet
att M är delbart med q men ej med p behandlas på
samma sätt.
.
Men detta gäller alltså bara under förutsättning att meddelandet
M varken är delbart med p eller q. Vi måste
också reda ut vad som gäller om M vore delbart med p eller
med q. Eftersom vi bara krypterar meddelanden M som är mindre
än pq så kan inte M vara delbart med både p
och q utan högst en av dem. Vi kan därför anta att
M är delbart med p, men ej med q. Fallet
att M är delbart med q men ej med p behandlas på
samma sätt.
Vi ska visa att
d.v.s. att ![]() är delbart med pq. Vi skriver om uttrycket genom att bryta ut M
och skriver detta
är delbart med pq. Vi skriver om uttrycket genom att bryta ut M
och skriver detta
där vi ser
att M är delbart med p enligt antagandet och att ![]() är delbart med q enligt antagandet att M ej är delbart
med q, ty analogt med resonemanget i (**) gäller
är delbart med q enligt antagandet att M ej är delbart
med q, ty analogt med resonemanget i (**) gäller
Alltså är
![]() delbart
med både p och med q och därför med produkten
N = pq eftersom p och q är primtal.
Vi har alltså visat att
delbart
med både p och med q och därför med produkten
N = pq eftersom p och q är primtal.
Vi har alltså visat att
om M är mindre än pq.
Vad
är egentligen Eulers phi-funktion?
Eulers phi-funktion ![]() definieras allmänt som antalet positiva heltal mindre än n som
är relativt primiska till n, d.v.s. antalet positiva heltal mindre
än n som inte har några gemensamma delare med n. T.ex.
får vi
definieras allmänt som antalet positiva heltal mindre än n som
är relativt primiska till n, d.v.s. antalet positiva heltal mindre
än n som inte har några gemensamma delare med n. T.ex.
får vi
Talen 1, 2 är relativt primiska till n = 3.
Talen 1, 2, 3, 4, 5, 6 är relativt primiska till n = 7.
Talen 1, 5 är relativt primiska till n = 6.
Hur beräknar
man ![]() ?
?
För vissa specialfall finns enkla metoder. Om p är primtal
så gäller
Om p och q är primtal så kan man visa att
![]() Läs mer om RSA på RSA
Security Inc. »
Läs mer om RSA på RSA
Security Inc. »
Om modulo-räkning
Om man ställer frågan
—"Hur mycket är klockan?"
så kan man exempelvis få svaret
—"Klockan är tre."
Om man ställer samma fråga nästa dag vid samma tid på dygnet eller efter en vecka vid samma tid på dygnet
—"Hur mycket är klockan?"
så får man samma svar
—"Klockan är tre."
Det är alltså ingen skillnad på om klockan är tre en dag eller om klockan är tre en annan dag. Vid midnatt har klockan nått fram till 24.00. Då börjar man räkna från 00.00 tills man har nått fram till 24.00 igen nästa midnatt och då börjar man om från 00.00 igen, o.s.v.
Den egenskap vi frågar efter är hur många timmar som gått, fast bara i förhållande till varje multipel av 24. Matematiskt så frågar vi alltså efter resten vid division med 24. Vi skulle kunna beskriva detta genom att säga att tiden är klockan 3 modulo 24.
Mycket i detta avsnitt bygger på modulräkning. Vi skriver
som utläses
"a är kongruent med b modulo n" och menar
då att a och b bildar samma rest vid division med n.
Detta innebär att ![]() för något heltal c.
för något heltal c.
a och b har samma rest vid division med n.
Man kan räkna med kongruenstecknet på ungefär samma sätt som vanligt likhetstecken. Följande räkneregler gäller:
Om
och
så gäller
|
|
Vi kan formulera några ytterligare räkneregler.
Om
och
och om K = minsta gemensamma multipeln till m och n så gäller
Speciellt gäller att om p och q är primtal att minsta gemensamma multipeln till p och q är pq. Därför följer från ovanstående räkneregel:
Om p och q är primtal så gäller
och
Man kan också visa följande strykningslag (ungefär som vid vanlig aritmetik):
Om p är ett primtal och om
så gäller