• Definition of Taylor polynomials
• Animation of Taylor series convergence
• Taylor remainder theorem

Taylor Series

Definition of Taylor polynomials

Suppose the nth derivative of is defined at . Then the nth Taylor polynomial for f at is defined as follows:

> p[n](x) = sum((D@@i)(f)(a)/i!*(x-a)^i,i=0..n);

The Taylor remainder function is defined as

>

Warning, premature end of input

There is a word, taylor , in the Maple vocabulary already which compute Taylor polynomials. Suppose we want the 11 th Taylor polynomial of the sin function at x = 0.

> p11 := taylor(sin(x),x=0,12);

p11 is not actually a polynomial because of the term at the end which is used to signal which polynomial is represented (in case some of the coefficients are 0). We can convert to a polynomial.

> p11 := convert(p11,polynom);

The Taylor polynomials are usually good approximations to the function near a. Let's plot the first few polynomials for the sin function at x =0.

> sinplot := plot(sin,-Pi..2*Pi,thickness=2):

> tays:= plots[display](sinplot):
for i from 1 by 2 to 11 do
tpl := convert(taylor(sin(x), x=0,i),polynom):
tays := tays,plots[display]([sinplot,plot(tpl,x=-Pi..2*Pi,y=-2..2,
color=black,title=convert(tpl,string))]) od:

> plots[display]([tays],view=[-Pi..2*Pi,-2..2]);

Animation of Taylor series convergence

The Taylor Polynomials gradually converge to the Taylor Series which is a representation of the original function in some interval of convergence. In this section, we'll see with our own eyes how this convergence takes place in an animation.

First we define a function and a generic Taylor polynomial. Then we define some constant so that our graph desplays for a =< x =< b, and c =<y =< d.

> restart; with(plots):

Warning, the name changecoords has been redefined

> f := x -> sin(x);

> on := x -> piecewise( x <0, 0, x < 1, 1,1);

> a := -6: b := 6: c := -3: d:= 4:

> g := (x,k) -> convert(series(f(x), x, k), polynom):

> display( plot( f(x), x = a..b, y = c..d, thickness = 3, color = blue), animate( on(t-1)*g(x,2) , x = a..b, t = 0..7, view = c..d, color = cyan), animate( on(t-2)*g(x,4) , x = a..b, t = 0..7, view = c..d, color = coral),animate( on(t-3)*g(x,6) , x = a..b, t = 0..7, view = c..d, color = green), animate( on(t-4)*g(x,8) , x = a..b, t = 0..7, view = c..d, color = violet), animate( on(t-5)*g(x,10) , x = a..b, t = 0..7, view = c..d, color = red), animate( on(t-6)*g(x,12) , x = a..b, t = 0..7, view = c..d, color = coral) );

>

Taylor remainder theorem

Theorem: (Taylor's remainder theorem) If the (n+1)st derivative of f is defined and bounded in absolute value by a number M in the interval from a to x, then

This theorem is essential when you are using Taylor polynomials to approximate functions, because it gives a way of deciding which polynomial to use. Here's an example.

Problem Find the 2nd Taylor polynomial p[2] of 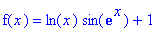at . Plot both the polynomial and f on the interval [.5,1.5]. Determine the maximum error in using p[2] to approximate ln(x) in this interval.

Solution:

> f := x -> ln(x)*sin(exp(x))+1;

> fplot := plot(f,.5..1.5,thickness = 2):

> p[2] := x -> sum((D@@i)(f)(1.)/i!*(x-1.)^i,i=0..2);

> p[2](x);

> t2 := unapply( convert(taylor(f(x),x=1,3),polynom),x);

> tplot := plot(t2,1..1.5,color=black):

> plots[display]([fplot,tplot]);

In order to use Taylor's remainder theorem, we need to find a bound M on the 3rd derivative of the function f. In this case, we could just plot the third derivative and eyeball an appropriate value for M.

> plot((D@@3)(f),.5..1.5) ;

We could use M = 75.

> M := 75;

So the remainder is bounded by

> M/3!*(1.5-1)^3;

We can see from the plot of f and the polynomial that the actual error is never more than about .1 on the interval [.5,1.5].

Another example :

Which Taylor polynomial would you use to approximate the sin function on the interval from -Pi to Pi to within 1/10^6?

Solution:

Well, 1 is a bound on any derivative of the sin on any interval. So we need to solve the inequality

> ineq := 1/n!*Pi^n <= 1/10^6;

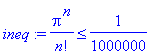
for n. Solve will not be much help here because of the factorial, but we can find the smallest n by running through a loop.

> n := 1: while evalf(1/n!*Pi^n) > 1/10^6 do n := n+1 od: print (`take n to be `,n);

> (seq(evalf( 1/n!*Pi^n) ,n=15..20));

> restart;

> t17 := convert(taylor(sin(x),x=0,18),polynom);

> plot(t17,x=-Pi..Pi);

Looks pretty much like the sin function.