Tid: 28 maj 1998 kl 1515-1700 (Observera dagen och tiden!)
Plats : Seminarierummet 3733, Institutionen för matematik, KTH, Lindstedts väg 25, plan 7. Karta!
Föredragshållare: Malcolm Quine, School of Mathematics and Statistics, University of Sydney. (Publikationslista)
Titel: Asymptotic Normality of Processes with a Branching Structure
Summary with link to complete paper
Sammanfattning:
Let 
be integer-valued rv's defined
on the same probability space 
and define
sequences 
and 
by
, 
, 
and
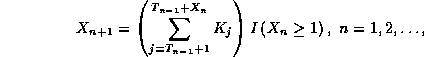
where 
denotes the indicator of 
.
The process 
contains the classical Bienaymé-Galton-Watson branching process as a special case, and is also relevant to urn models and to a
`self-annihilating branching process' considered by
Erickson (Ann. Probab. 1973) as a model for the antigenic behaviour of Lymphoma cell
populations.
We will first review the results of Quine and Szczotka (Ann. Appl. Probab. 1994)
concerning the extinction probability 
and
the asymptotic behaviour of 
and 
, when 
, including
1)
the a.s. convergence of
to some non-negative rv 
as 
, for some constant 
and
2) when 
, rate of convergence results of the form
and
where 
is a standard normal rv independent of
, for some 
.
We will then discuss further unpublished joint work with Szczotka, investigating the extent to which and share similar asymptotic properties.
For instance we consider the analogues for the sequence
, and establish an equivalence relation between these
convergences. We show that
in some situations the rate is Gaussian or mixed
Gaussian.
We also investigate the asymptotic
behaviour of 
(or 
) when the centering involves
the limit rv .
Some of the results we obtain in this paper are known in the B-G-W
case. However, our approach here is far more general: the summands
need be neither independent nor identically distributed
(nor even non-negative). Our approach uses probabilistic methods
based on an underlying Wiener process rather than methods based on
p.g.f.'s or characteristic functions.
