
Tid: 19 april 1999 kl 1515-1700
Plats : Seminarierummet 3733, Institutionen för
matematik, KTH, Lindstedts väg 25, plan 7. Karta!
Föredragshållare:
Laurent Decreusefond, Ecole nationale supérieure des
télécommunications, Paris.
Titel:
A functional central limit theorem for fractional Brownian motion.
Sammanfattning:
Abstract in Postscript format
A result of Fouque (1984) stands that for a standard
Brownian motion B, the
sequence of 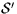 -valued processes
-valued processes
![\begin{displaymath}
S_t^n= \frac{1}{\sqrt{n}}\sum_{j=1}^n(\epsilon _{B_t^j}-E[\epsilon_{B_t^j}]),\end{displaymath}]( ./990419/img2.gif)
where 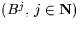 are independent copies of B,
converges in distribution to a generalized Ornstein-Uhlenbeck
process. The main ingredients in this work are general result on
convergence in nuclear spaces and the Itô
formula. The problem addressed here is to generalize this result when
the standard Brownian motion is replaced by a fractional Brownian
motion of Hurst index in
are independent copies of B,
converges in distribution to a generalized Ornstein-Uhlenbeck
process. The main ingredients in this work are general result on
convergence in nuclear spaces and the Itô
formula. The problem addressed here is to generalize this result when
the standard Brownian motion is replaced by a fractional Brownian
motion of Hurst index in 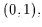 denoted by
denoted by 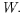 Since
Since 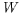 is
not a semi-martingale and that an Itô formula does not exist for
is
not a semi-martingale and that an Itô formula does not exist for
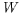 when
when 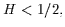 the method of Fouque can not be straightforwardly applied.
The difficulty is bypassed by considering a sample-path
valued semi-martingale
the method of Fouque can not be straightforwardly applied.
The difficulty is bypassed by considering a sample-path
valued semi-martingale 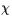 , namely
, namely
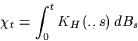
(where 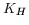 is defined in order that
is defined in order that
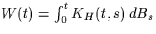 )
which is such that
)
which is such that 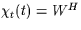 and for which one can write an
Itô formula. The methods of Fouque are then
applicable to
and for which one can write an
Itô formula. The methods of Fouque are then
applicable to 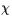 so that we can solve our original problem and
show that
so that we can solve our original problem and
show that
![\begin{displaymath}
\frac{1}{\sqrt{n}}\sum_{j=1}^n(\epsilon _{W_t^j}-E[\epsilon_{W_t^j}]),\end{displaymath}]( ./990419/img13.gif)
converges weakly in 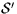 to a time changed
generalized Ornstein-Uhlenbeck process.
to a time changed
generalized Ornstein-Uhlenbeck process.
Till seminarielistan
To the list of
seminars


![]() -valued processes
-valued processes
![\begin{displaymath}
S_t^n= \frac{1}{\sqrt{n}}\sum_{j=1}^n(\epsilon _{B_t^j}-E[\epsilon_{B_t^j}]),\end{displaymath}]( ./990419/img2.gif)
![]()
![\begin{displaymath}
\frac{1}{\sqrt{n}}\sum_{j=1}^n(\epsilon _{W_t^j}-E[\epsilon_{W_t^j}]),\end{displaymath}]( ./990419/img13.gif)