Kurs 5B1200, Sammanfattningar av lektioner för M2 läsåret 1998/99.

Björn Gustafsson

Lektion 1

En separabel differentialekvation är en som kan skrivas på formen

f(x)dx = g(y)dy.

Lösningar på implicit form fås genom direkt integration:

$$\int f(x)dx = \int g(y)dy.$$

Ofta måste man dividera med okända funktioner. Glöm ej bort lösningar som förloras vid division med noll.

En linjär differentialekvation av 1:a ordningen är en som kan skrivas

y' + f(x) y = g(x).

Den kan göras exakt, dvs direkt integrerbar, genom multiplikation med den integrerande faktorn e^F(x), där F'(x) = f(x).

----------------------------------

Lektion 2

Ibland kan en differentialekvation återföras till en känd typ med hjälp av en substitution (variabeltransformation) av den beroende eller oberoende variabeln. Exempel på sådana fall är

1) "homogena" ekvationer, dvs. ekvationer av typ

y'=f(y/x),

som blir separabla med u=y/x som ny beroende variabel (i stället för y), samt

2) "Bernoullis" ekvation

y' + f(x) y = g(x) y^a,

som blir linjär i den nya beroende variabeln u=y^1-a. (Här antas $a\ne 1$; om a=1 är ekvationen linjär redan från början).

--------------------------------

Lektion 3

Existens och entydighet för lösningar till första ordningens differentialekvationer: antag att en differentialekvation

F(x,y,y')=0

kan skrivas på normalform

y'=f(x,y).

Om då funktionen f(x,y) och dess förstaderivata $\partial f/\partial y$ är kontinuerliga i ett område D av xy-planet så passerar precis en lösningskurva y=y(x) genom varje punkt i D.

-----------------------------

Lektion 4

Vid lösandet av"benämnda uppgifter" är det viktigt att kontrollera att de uppnådda resultaten är rimliga i sammanhanget ifråga.

------------------------------

Lektion 5

En linjär differentialekvation av ordning n är en ekvation som kan skrivas på formen

$$a_n(x)y^{(n)}+a_{n-1}(x)y^{n-1}+\dots +a_1(x)y'+a_0(x)y = g(x).$$

Ofta används det mera kortfattade skrivsättet

L(D)y=g,

där $D=\frac{d}{dx}$. Lineariteten innebär att operatorn L(D) bevarar linjärkombinationer: L(D)(c₁y₁+c₂y₂)=c₁L(D)y₁+c₂L(D)y₂ (c_j konstanter, y_j funktioner).

Om koefficienterna a_j(x) och högerledet g(x) är kontinuerliga på ett intervall I och a_n(x) är skild från noll där, så har den allmänna lösningen strukturen

$$y(x)=y_H(x)+y_P(x) = c_1y_1(x) +\cdots +c_ny_n(x) + y_P(x).$$

Här är y_H är den allmänna homogena lösningen (dvs. allmänna lösningen till L(D)y=0), y_P en partikulär lösning (dvs en lösning, vilken som helst, till L(D)y=g) och samtliga funktioner är definierade på hela I. Funktionerna $y_1,\cdots ,y_n$ utgör en fundamental lösningsmängd (bas för lösningarna) till den homogena ekvationen. Speciellt är de linjärt oberoende, dvs. ingen av dem kan uttryckas som en linjärkombination av de övriga.

Givet $x_0\in I$ och värden $y_0, \cdots ,y_{n-1}$ så kan konstanterna $c_1 ,\cdots c_n$ bestämmas entydigt, via lösandet av ett linjärt ekvationssystem, så att lösningen uppfyller begynnelsevillkoret

$$y(x_0)=y_0,\,\, y'(x_0)=y_1,... ,y^{(n-1)}(x_0)=y_{n-1}.$$

Determinanten för matrisen till ekvationssystemet i fråga är den s.k. Wronskideterminanten $W(y_1,\cdots, y_n)(x_0)$för funktionerna $y_1,\cdots ,y_n$ i punkten x₀.

För Wronskideterminanten till en godtycklig uppsättning av n stycken homogena lösningar gäller att den antingen är lika med noll på hela intervallet I, eller också aldrig noll (på I), och det senare inträffar om och endast om lösningarna är linjärt oberoende och därmed utgör en fundamental lösningsmängd.

---------------------------------

Lektion 6

För en linjär ekvation

L(D)y = g

med konstanta koefficienter erhålls en fundamental lösningsmängd till motsvarande homogena ekvation genom lösning av den karakteristiska ekvationen

L(r)=0.

För varje rot r till denna fås en baslösning e^rx. Om r råkar vara vara en multipel rot, av multiplicitet m, så genererar den m baslösningar, nämligen e^rx, xe^rx,...,x^m-1e^rx. Ovanstående gäller även i fallet icke-reella karakteristiska rötter, varvid lösningarna skrivs på reell form med hjälp av relationen

$$e^{(\alpha +i\beta)x}= e^{\alpha x}(\cos \beta x + i\sin \beta x).$$

Om högerledet g är en kombination av exponentialfunktioner och polynom, så finns normalt en partikulärlösning av samma typ, som erhålls genom ansats: för en term

$$e^{\alpha x}(A\cos\beta x + B\sin\beta x)\cdot (C_0 + C_1 x + \cdots +C_n x^n)$$

i g(x) ansätts

$$e^{\alpha x}(a\cos\beta x + b\sin\beta x)\cdot (c_0 + c_1 x+ \cdots +c_n x^n),$$

där a, b, c₁,...,c_n ska bestämmas. (Om en av A och B är lika med noll så måste ändå både a och b vara med i ansatsen.)

Det kan inträffa att ansatsen ovan misslyckas, nämligen om $\alpha + i \beta$ råkar vara en karakteristisk rot ("resonans"). Då ändras ansatsen till

$$x^m e^{\alpha x}(a\cos\beta x + b\sin\beta x)\cdot (c_0 + c_1 x+ \cdots +c_n x^n),$$

där m är multipliciteten för roten.

--------------------------------

Lektion 7

Andra metoder för bestämning av partikularlösning till en linjär ekvation L(D)y=g är

1) Reduktion av ordning: Antag att en homogen lösning y₁ är känd. Då leder ansatsen y=uy₁ (för den fullständiga ekvationen) till en linjär differentialekvation för u som innehåller u:s derivator men inte u själv. Alltså kan v=u' införas som ny beroende variabel, varvid ekvationens ordning reduceras med en enhet.

En 2:a ordningens linjär differentialekvation kan därmed lösas fullständigt om man känner en homogen lösning.

2) Variation av parametrar. Om hela den homogena lösningen

y_H (x)=c₁y₁(x)+...+c_ny_n(x)

är känd så ansätts för den inhomogena ekvationen

y(x)=u₁(x)y₁(x)+...+u_n(x)y_n(x),

där u₁,...,u_n är de tidigare konstanterna, som nu tillåts variera. Om man kräver att de ska vara "så konstanta som möjligt", i meningen att

u₁'(x)y₁(x)+...+u_n'(x)y_n(x)=0,

u₁'(x)y₁'(x)+...+u_n'(x)y_n'(x)=0,

...

u₁'(x)y₁^(n-2)(x)+...+u_n'(x)y_n^(n-2)(x)=0,

så fås ett linjärt ekvationssystem i u₁',...,u_n', som kan lösas rutinmässigt, varefter u₁,...,u_n, och därmed y, fås efter integration. Jämför motsvarande metod för system, lektion 19.

3) Laplacetransformering, se nedan.

------------------------------

Lektion 8-9

Laplacetransformen för en funktion f(t) definierad för $t\geq 0$ (t är typiskt en tidsvariabel) är funktionen

$${\mathcal L}(f(t))(s)= F(s)=\int_0^\infty f(t)e^{-st} dt.$$

Den definierad på ett intervall av typen s>c, där c är ett tal som beror på f. Laplacetransformens viktigaste egenskap är att den omvandlar operationen "derivation med avseende på t" till den mycket enklare operationen "multiplikation med s" (väsentligen), nämligen

$${\mathcal L}(f'(t)) = sF(s)-f(0),$$

där $F={\mathcal L}(f)$. Denna egenskap gör att linjära differentialekvationer (med konstanta koefficienter) omvandlas till algebraiska ekvationer då de Laplacetransformeras, och därigenom blir lätta att lösa på transformsidan. Motsvarande gäller för vissa typer av integralekvationer. Återtransformering ${\mathcal L}^{-1}$ till ursprungssidan kan vara besvärlig (underlättas av god tabell), men är alltid möjlig i princip på grund av en entydighetssats: Om ${\mathcal L}(f)={\mathcal L} (g)$så gäller f=g (utom möjligen på en "nollmängd").

Några andra viktiga allmänna egenskaper hos Laplacetransformen är att den omvandlar translation ($t\mapsto t-a$) till multiplikation med en exponentialfaktor, och omvänt:

$${\mathcal L}(f(t-a)H(t-a)) = e^{-as}F(s) \quad {\rm om}\quad a\gt,$$

$${\mathcal L}(e^{-at}f(t))=F(s+a).$$

Här är H Heaviside's språngfunktion ("unit step function"): H(t)=0 för t<0, H(t)=1 för $t\geq 0$.)

--------------------------------

Lektion 10

Laplacetransformen är en linjär transformation, dvs den bevarar linjärkombinationer av funktioner:

$${\mathcal L}(af(t)+bg(t))=a{\mathcal L}(f(t))+b{\mathcal L}(g(t))$$

om a, b är konstanter. Däremot bevarar den inte multiplikation mellan funktioner. Multiplikation på tranformsidan svarar mot faltning på ursprungssidan:

$${\mathcal L}(f*g)= {\mathcal L}(f)\cdot {\mathcal L}(g),$$

där

$$(f*g)(t)=\int_0^\infty f(\tau)g(t-\tau)d\tau.$$

Den multiplikativa enheten på transformsidan, nämligen funktionen F(s)=1, svarar mot Diracs deltafunktion $\delta (t)$ på ursprungssidan: ${\mathcal L}(\delta)= 1$.Det följer att $\delta (t)$ är enhet med avseende på faltning: $f=f*\delta =\delta *f$.

---------------------------------

Lektion 11

En funktion f(t) som är periodisk, med period T>0 (dvs f(t)=f(t+T) för alla t), kan utvecklas i en Fourierserie,

$$f(t)={a_0\over 2}+\sum_{n=1}^\infty (a_n\cos n\Omega t +b_n \sin n\Omega t),$$

där $\Omega =2\pi /T$ är vinkelfrekvensen och där Fourierkoefficienterna a_n, b_n ges av

$$a_n={2\over T} \int_c^{c+T} f(t)\cos n\Omega t \,dt \quad (n\geq 0),$$

$$b_n={2\over T} \int_c^{c+T} f(t)\sin n\Omega t \,dt \quad (n\geq 1)$$

för godtyckligt c.

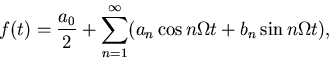
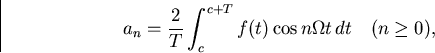
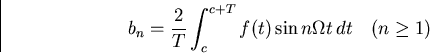
Om f är styckvis kontinuerligt deriverbar så konvergerar partialsummorna i Fourierserien mot f(t) i varje punkt t i vilken f är kontinuerlig, och mot (f(t+)+f(t-))/2, dvs. medelvärdet av höger- och vänstergränsvärdena, om t är en diskontinuitetspunkt.

Fourierserierepresentationen ovan gäller också om f bara är definierad på ett intervall (c,c+T) av längd T, ty f kan då alltid utvidgas till en T-periodisk funktion på hela reella linjen. Observera dock att punkterna c, c+T osv. blir diskontinuitetspunkter för den periodiska utvidgningen om $f(c)\ne f(c+T)$.

---------------------------

Lektion 12

Om en funktion f(t) är definierad på ett intervall (0,T) så finns det tre naturliga Fourierserierrepresentationer av f, nämligen de som svarar mot följande periodiska utvidgningar av f till hela reella linjen:

1) Direkt utvidgning till T-periodisk funktion (se Lektion 11).

2) Utvidgning först till en jämn funktion på intervallet (-T,T), därefter utvidgning av denna som 2T-periodisk funktion.

3) Utvidgning först till en udda funktion på intervallet (-T,T), därefter utvidgning av denna som 2T-periodisk funktion.

Metod 2) ger cosinusserien för f:

$$f(t)={a_0\over 2}+ \sum_{n=1}^\infty a_n \cos {n\pi t\over T},$$

där

$$a_n={2\over T}\int_0^T f(t)\cos{n\pi t\over T}\, dt.$$

Metod 3) ger sinusserien för f:

$$f(t)=\sum_{n=1}^\infty b_n \sin {n\pi t\over T},$$

där

$$b_n={2\over T}\int_0^T f(t)\sin {n\pi t\over T}\, dt.$$

--------------------------------

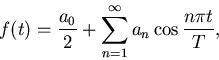
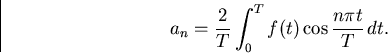
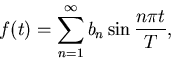
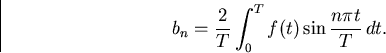
Lektion 13

Typiska rand/begynnelsevärdesproblem för partiella differentialekvationer i rektangulära områden är

Värmeledningsekvationen:

$${\partial u\over \partial t}=k {\partial^2 u\over \partial x^2} \quad {\rm f\uml or}\quad 0<x<L,\,\, t\gt,$$

$${\rm BV: }\quad u \quad {\rm given \,\,f\uml or} \quad t=0,$$

$${\rm RV: } u\,\, \quad {\rm given\,\, f\uml or }\quad x=0, \,\,x=L.$$

Vågekvationen:

$${\partial^2 u\over \partial t^2}=c^2 {\partial^2 u\over \partial x^2} \quad {\rm f\uml or} \quad 0<x<L,\,\, t\gt,$$

$${\rm BV: }\quad u \quad {\rm och}\quad {\partial u\over \partial t} \quad {\rm givna \,\,f\uml or} \quad t=0,$$

$${\rm RV: } u \quad {\rm given\,\,f\uml or }\quad x=0, \,\,x=L.$$

Laplace ekvation:

$${\partial^2 u\over \partial x^2}+{\partial^2 u\over \partial y^2}=0 \quad {\rm f\uml or}\quad 0<x<a,\,\, 0<y<b,$$

$${\rm RV: \quad } u \quad {\rm \,\,given\,\, p{\aa}\,\, hela\,\, randen.\,\,}$$

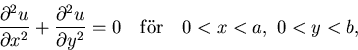
I randvillkoren ovan kan, istället för u dess normalderivata ${\partial u\over \partial n}$ vara given på en del av randen.

--------------------------------

Lektion 14-15

Variabelseparationsmetoden för lösning av rand/begynnelsevärdesproblem som ovan (Lektion 13):

Man söker först funktioner på formen

u(x,t)=X(x)T(t)

(u(x,y)=X(x)Y(y) i fallet Laplace ekvation) som löser differentialekvationen samt uppfyller de homogena rand/begynnelsevillkoren (dvs. de villkor som är på formen att u eller någon derivata av u är lika med noll).

Differentialekvationen själv ger upphov till likheter av typen (vi tar värmeledningsekvationen som exempel)

$${X''(x)\over X(x)} = {T'(t)\over kT(t)}= {\rm konstant} =c,$$

och de homogena rand/begynnelsevillkoren tillåter vanligtvis sedan icke-triviala lösningar till denna ekvation endast för vissa speciella värden på c, säg c₁, c₂,... (en sorts egenvärden).

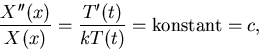
Om X_n(x), T_n(t) är tillhörande lösningar (bestämda upp till konstanta faktorer) så är, utöver u_n(x,t)=X_n(x)T_n(t), även alla linjärkombinationer

$$u(x,t)=\sum_{n=0}^\infty a_nX_n(x)T_n(t)$$

lösningar till differentialekvationen och de homogena rand/begynnelsevillkoren.

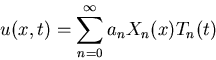
Slutligen anpassas koefficienterna a_n i denna utveckling så att övriga rand/begynnelsevillkor blir uppfyllda. Detta brukar leda till att a_n ska identifieras med lämpliga Fourierkoefficienter för rand/begynnelsefunktionerna.

--------------------------------

Lektion 16

Ett linjärt system av 1:a ordningens differentialekvationer skrivs med fördel på matrisform

X'(t)=A(t)X(t)+F(t),

där A(t) är en matris och X(t), F(t) kolonnvektorer, som alla är funktioner av den oberoende variabeln t. Om A(t) och F(t) har storlek $n\times n$respektive $n\times 1$ och är kontinuerliga på ett intervall I så finns, givet $t\in I_0$ och en startvektor X₀, precis en lösning X(t) (storlek $n\times 1$)som löser systemet på intervallet I och som uppfyller begynnelsevillkoret

X(t₀)=X₀.

Den allmänna lösningen till systemet utan begynnelsevillkor har strukturen

X(t)=X_H(t)+X_P(t)=c₁X(t)₁+...+c_nX_n(t)+X_P(t),

där X₁(t),...,X_n(t) är linjärt oberoende lösningar till motsvarande homogena problem (dvs det med F=0).

En lösningsfamilj X₁(t),...,X_n(t) som ovan kallas fundamental lösningsmängd, och matrisen $\Phi(t)$med dem som kolonner fundamentalmatris (för systemet X'=AX). Determinanten

$$W(t)=\det \Phi(t)$$

kallas Wronskideterminanten.

Om X₁(t),...,X_n(t) är homogena lösningar vilka som helst så gäller att de är linjärt oberoende (eller en fundamental lösningsmängd) om och endast om motsvarande Wronskideterminant är skild från noll (i en punkt eller, vilket blir samma sak, i alla punkter).

----------------------------------

Lektion 17-18

Ett homogent linjärt system med konstanta koefficienter

X'(t)=AX(t)

löses via ansatsen $X(t)=Ke^{\lambda t}$,där K är en konstant vektor skild från noll och $\lambda$ett reellt eller komplext tal.

Insättning av ansatsen ger att X(t) är en lösning om och endast om

$$AK=\lambda K,$$

dvs $\lambda$ är ett egenvärde till matrisen A och K en tillhörande egenvektor. Egenvärdena fås direkt ur karakteristiska ekvationen

$$\det (A-\lambda I)=0$$

(I är enhetsmatrisen), och tillhörande K fås sedan ur $AK=\lambda K$.

Olika egenvärden $\lambda$ ger linjärt oberoende lösningar X(t), så om A har n stycken skilda reella egenvärden $\lambda_1,...,\lambda_n$ så blir den fullständiga lösningen till differentialekvationen

$$X(t)=c_1 e^{\lambda_1 t}K_1+...+c_n e^{\lambda_n t}K_n.$$

Följande komplikationer kan dock inträffa:

1) Det förekommer icke-reella egenvärden. Detta förändrar ingenting i princip, men lösningen måste skrivas på reell form (A antas reell). Om $\lambda=\alpha +i\beta$ är ett icke-reellt egenvärde och K=B₁ +i B₂ en tillhörande egenvektor så är real- och imaginärdelarna

$$Re(e^{\lambda t}K) =[B_1\cos \beta t -B_2 \sin \beta t] e^{\alpha t},$$

$$Im(e^{\lambda t}K) =[B_1\sin \beta t +B_2 \cos \beta t] e^{\alpha t},$$

var för sig lösningar (observera att vi i själva verket har två egenvärden, $\alpha \pm i \beta$).

2) Karakteristiska ekvationen har multipla rötter. Om $\lambda$ exempelvis är dubbelrot till KE så producerar den ändå två baslösningar, så här:

Fall 2a) Det finns två linjärt oberoende egenvektorer, K₁ och K₂, till $\lambda$. Då blir baslösningarna

$$K_1 e^{\lambda t}, \quad K_2 e^{\lambda t}.$$

Fall 2b) Det finns endast en egenvektor, K, till $\lambda$.I så fall finns också en s.k. generaliserad egenvektor, P, definierad genom ekvationen

$$(A-\lambda I) P =K.$$

De två baslösningarna hörande till $\lambda$ blir nu

$$K e^{\lambda t}, \quad (K t + P)e^{\lambda t}.$$

----------------------------------

Lektion 19

Om X₁,...,X_n är en fundamental lösningsmängd till ett linjärt system X'=AX så kan den allmänna lösningen X(t)=c₁X₁(t)+...+c_nX_n(t) skrivas på matrisform som

$$X(t)=\Phi (t) C.$$

Här är C är kolonnvektorn med konstanterna c₁,...,c_n som komponenter och $\Phi(t)$ är matrisen med vektorerna X₁(t),...X_n(t) som kolonner. En sådan matris $\Phi(t)$kallas fundamentalmatris till systemet. Den är alltid icke-singulär och uppfyller

$$\Phi'(t)=A\Phi(t).$$

Metoden "variation av parametrar" för lösning av det inhomogena problemet

X'=AX+F

(F=F(t)) innebär att man gör ansatsen

$$X(t)=\Phi (t)U(t),$$

där vektorn U(t) ska bestämmas. Detta leder till $U(t)=\int\Phi^{-1}F(t)\,dt+C,$ dvs

$$X(t)=\Phi(t)(\int\Phi(t)^{-1}F(t)\,dt +C).$$

Även Laplacetransformering är en mycket användbar metod för att lösa system X'=AX+F, särskilt om begynnelsevektorn X(0) är given.

-----------------------------------

Lektion 20-21

Här studeras autonoma dynamiska system

X'(t)=g(X(t)),

där g är en (i allmänhet icke-linjär) funktion $g:{\bf R}^n\rightarrow{\bf R}^n$. Rummet ${\bf R}^n$ kallas i detta sammanhang fasrummet och g uppfattas lämpligen som ett vektorfält. Lösningar X(t) till systemet blir tidsparametriserade kurvor i fasrummet, som kallas fastrajektorier (eller faskurvor, eller banor helt enkelt). Om g är kontinuerligt deriverbar (antas alltid) så passerar exakt en fastrajektoria genom varje punkt i fasrummet, enligt en högredimensionell motsvarighet till existens- och entydighetssatsen i Lektion 3.

Lösningarna kan delas in i

1) jämviktslösningar, dvs konstantlösningar: X(t)=X₀ för alla t och något $X_0\in{\bf R}^n$. Punkten X₀ kallas då jämviktspunkt, eller kritisk punkt.

2) periodiska lösningar, dvs icke-jämviktslösningar sådana att det finns en periodtid T>0 så att X(t+T)=X(t) för alla (ekvivalent: något) t.

3) Övriga lösningar, dvs lösningar som aldrig kommer tillbaka till samma punkt.

Omedelbart inses att $X_0\in{\bf R}^n$ är en kritisk punkt om och endast om

g(X₀)=0.

En kritisk punkt X₀ kallas stabil om varje trajektoria som kommer tillräckligt nära X₀ stannar kvar i närheten av X₀ i evighet. I annat fall är den instabil. Om X₀ är stabil och dessutom varje trajektoria X(t) som kommer tillräckligt nära X₀ verkligen sugs in i X₀ (dvs $X(t)\rightarrow X_0$ då $t\rightarrow \infty$)så kallas X₀ asymptotiskt stabil.

För linjära system, dvs då g(X)=AX för någon matris A, är origo alltid en kritisk punkt. Om $\det A\ne 0$ så är origo den enda kritiska punkten. Linjära system av dimension n=2 och med $\det A\ne 0$ kan klassificeras enligt följande, i termer av egenvärdena $\lambda_1$, $\lambda_2$ till A, eller alternativt i termer av A:s determinant $\Delta$ och spår $\tau$ (summan av diagonalelementen). Sambanden är

$$\lambda^2 -\tau\lambda +\Delta =0, \quad \lambda=(\tau\pm\sqrt{\tau^2-4\Delta})/2,$$

$$\Delta=\lambda_1\lambda_2, \quad \tau=\lambda_1+\lambda_2.$$

Stabilitet: Origo är asymptotiskt stabil om båda egenvärdena är strängt negativa, instabil om något av dem är strängt positivt.

Typ av kritisk punkt:

Fall 1. Reella skilda egenvärden, ekvivalent $\tau^2-4\Delta \gt:$

Om egenvärdena har samma tecken så är origo en nod

Om egenvärdena har olika tecken så är origo en sadelpunkt.

Fall 2. Två lika reella egenvärden, ekvivalent $\tau^2-4\Delta =0:$Origo är en degenererad nod. Om det finns två linjärt oberoende egenvektorer så är fasporträttet rotationssymmetriskt, och man kallar också origo för en stjärna.

Fall 3. Komplexa egenvärden, dvs $\tau^2-4\Delta<0:$Egenvärdena bildar ett komplexkonjugerat par. Om de ligger på imaginäraxeln så är origo ett centrum, som är en stabil, men icke asymptotiskt stabil, kritisk punkt.

Om de ej ligger på imaginäraxeln så är origo en spiralpunkt.

Ett icke-linjärt system kan approximeras med linjära system i närheten av varje given punkt i fasrummet. Den linjära approximationen vid en kritiskt punkt ger vanligtvis en god bild av fasporträttet även för det icke-linjära systemet.

Låt X₀ vara en kritisk punkt till X'=g(X) och låt A=g'(X₀) vara Jacobimatrisen till g(X) i X₀. Då är den linjära approximationen till systemet vid X₀ helt enkelt

Y'(t)=AY(t),

där Y är den lokala variabeln Y=X-X₀. Alltså undersöks typ och stabilitet med hjälp av A som ovan.

SLUT