Exempel på användning av Nyquists metod och Maple.

De följande två exemplen är avsedda att ge stöd för lösningen av Inlämningsuppgifterna 1b och 2b i Komplex Analys för E, F och T .

Först några allmänna Maple-tips:

• Man tilldelar värden med := och avslutar kommandon med ; eller :.
• Kommandon exekveras med ett <return>. Visaren skall då befinna sig i anslutning till kommandot.
• Om kommandot avslutas med ; sker en utskrift i blå text av resultatet av exekveringen.
  Om kommandot avslutas med : sker ingen sådan utskrift.
• Kommandon kan grupperas i sektioner, som avgränsas av hakparenteserna i vänstermarginalen. Om visaren befinner sig inom en viss sektion exekveras alla kommandon i sektionen vid <return>.
• Om man använder <shift-return> exekveras inga kommandon utan man kan fortsätta att skriva nya kommandon i samma sektion.
• Vill man börja på en ny sektion flyttar man visaren till en position utanför den sektion man befinner sig i.
• Man kan gå tillbaka och ändra parametervärden och sedan exekvera på nytt.
  (I exemplen nedan sker dock inte detta eftersom beräkningsgången då kan bli svår att följa.)
  Även normal klipp- och klistringsteknik (copy, cut, paste) kan användas. (Finns under Edit).
• Ordningsföljden mellan exekveringarna kan ha betydelse. Är man osäker på vilka värden olika parametrar har för tillfället kam man exekvera restart-kommandot och börja om från början.

Exempel 1

Detta exempel ansluter sig till uppgift 1 i Inlämningsuppgiften. Problemet är att avgöra hur många nollställen polynomet
f(z) = 4 z³ - 2 z² + 3 z + 7 har i högra halvplanet.

Vi använder Maple och Nyquists metod:

> restart;
with(plots,conformal):

Börja alltid med restart.
':' efter andra raden i st. f. ';' förhindrar onödig textoutput.

Vi definierar nu tredjegradspolynomet f(z).

> a:=4;b:=-2;c:=3;q:=7;
f:=z-> a*z^3+b*z^2+c*z+q;

Nu skriver vi ut plottningskommandot:

> m:=5;
conformal(z,z=-m-m*I..m+m*I, grid=[2,2] );

Parametern 2 i grid-kommandot anger att en kvadrat avbildas (2 lodräta och 2 vågräta sträckor).

Parametern m anger hur stor denna kvadrat är.(Nedre vänstra hörnet : -m-mi, övre högra : m+mi.

Observera att det komplexa 'i' anges med 'I'.

Vi försöker med m=5 och ser efter hur kvadraten ser ut:

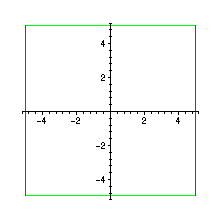
Man ser att Maple färgar lodräta sträckor röda och vågräta gröna.

Nu ser vi efter hur f(z) transformerar denna kvadrat:

(Notera att 'z' ersätts med 'f(z)' i första positionen:)

> m:=5;
conformal(f(z),z=-m-m*I..m+m*I, grid=[2,2] );

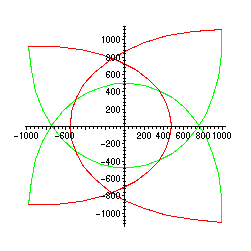
Lägg märke till att de röda och gröna kurvdelarna svarar mot motsvarande delar av kvadraten.

Vi ska nu räkna antalet varv runt origo. Eftersom f(z) är ett 3:egradspolynom vill vi hitta 3

stycken nollställen inom den givna kvadraten.

Antalet nollställen inom kvadraten skall ju enligt argumentprincipen vara = antal varv

som den transformerade kvadratens rand omkretsar origo.

Här syns det ganska tydligt att det blir 3 varv.

Vi kanske därför kan pröva om alla tre nollställen ligger inuti en ännu mindre kvadrat.

Vi försöker med m=3:

>

> m:=3;
conformal(f(z),z=-m-m*I..m+m*I, grid=[2,2] );

OK! 3 varv nu också.

Vi kan därför i fortsättningen använda denna kvadrat.

Nu vill vi se hur många nollställen som finns i högra halvplanet.

Vi ändrar därför kvadraten till den rektangel som utgör kvadratens del i

högra halvplanet..

Samtidigt lägger vi in kommandot 'view' med en parameter 'M' som gör det

lätt att snabbt ändra koordinataxlarnas skalor.

> m:=3;
M:=300;
conformal(f(z),z=-m*I..m+m*I, grid=[2,2] , view=[-M..M,-M..M]);

Lägg märke till här hur rektangelns hörn har ändrats i conformalkommandot (z = ... osv)!

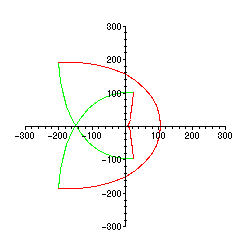
Här verkar det inte fullt klart hur

kurvan ser ut nära origo. Vi förstorar upp området nära origo genom att ge M värdet 20:

> M:=20;
conformal(f(z),z=-m*I..m+m*I, grid=[2,2] , view=[-M..M,-M..M]);

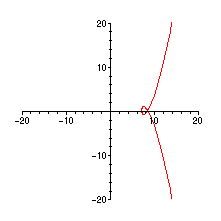
OK! Nu syns det klart att kurvan håller sig till höger om origo. Vi kan räkna till 2 varv runt origo och därmed 2 nollställen i den högra delen av kvadraten.

Men eftersom denna kvadrat innehöll alla tre nollställena vet vi att det finns 2 nollställen i det högra halvplanet.

Därmed är uppgiften löst.

Anm: Ibland behöver man öka antalet plottningspunkter för att få pålitliga kurvor efter en uppförstoring.

Inom kommandot 'conformal' sker detta genom ' numxy=[N,M]' där de hela talen N och M har default-värdet 15.

Försök med N=M=100.

numxy-kommandot används på samma sätt som grid och view. Kom ihåg kommat mellan dessa kommandon.

Inom kommandot 'plot' (som blir aktuellt i nästa exempel) används istället ' numpoints = N', där N=50 är default.

Exempel 2.

Detta exempel ansluter sig till uppgift 2 i Inlämningsuppgiften.

Vi betraktar den analytiska funktionen

g(z) = z⁴ + e^z + 5iz + 13.

Med Rouchées sats kan man visa att g(z) har 4 nollställen inom cirkeln med centrum i origo och med radien = 3.

Vi skall nu m.hj.a. Maple och Nyquist försöka hitta den största cirkeln med centrum i origo som bara innehåller 3 nollställen.
Man inser kanske att radien till denna cirkel är ungefär lika med avståndet från origo till det mest avlägsna nollstället.
Vi söker bland cirklar vars radier har två decimaler.

Vi behöver alltså plotta bilden av cirklar med olika radier r under transformationen g(z):

> restart;
with(plots,conformal):

Den vanliga inledningen.

>
a:=5;b:=13;
g:=z->z^4+ exp(z)+I*a*z+b;

Här har vi definierat funktionen g(z).

r:=3;
assume(t,real);
G:=evalc(subs(z=r*exp(I*t),g(z))):

Notera att t måste definieras som ett reellt tal.
Vi har nu satt in uttrycket för en cirkel med centrum i
origo och med radien r=3 (z=3e^it ) i funktionen g(z).
G(t) ger alltså den transformerade kurvan då t går från 0 till pi.

>
u:=Re(G):
v:=Im(G):

Real- och imaginärdelen av G(t) behövs i plottningskommandot.

n:= 150;
plot([u,v,t=0..2*Pi],view=[-n..n,-n..n]);

Här är plottningskommandot som plottar kurvan z = G(t), dvs:

x=u(t)

y=v(t), då t går från 0 till 2*pi.

Vi också lagt in 'view' för att kunna förstora upp kurvan

om det behövs.

Plottning med r=3 och view-parametern n= 150 ger:

Man ser här direkt att

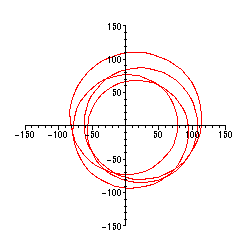
alla varv (4 st) omkretsar origo.

Alla nollställen ligger tydligen inom cirkeln med radien 3.

(Värdet n=150 för view-parametern får man pröva sig fram till).

Vi försöker igen med en mindre cirkel. r=2:

> r:=2;
assume(t,real);
G:=evalc(subs(z=r*exp(I*t),g(z))):

u:=Re(G):
v:=Im(G):

n:= 150;
plot([u,v,t=0..2*Pi],view=[-n..n,-n..n]);

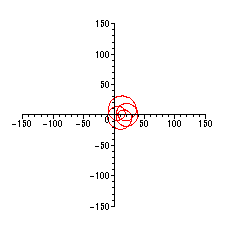
Kurvan är här för liten. Vi får minska view-parametern till 40:

> r:=2;
assume(t,real);
G:=evalc(subs(z=r*exp(I*t),g(z))):

u:=Re(G):
v:=Im(G):

n:= 40;
plot([u,v,t=0..2*Pi],view=[-n..n,-n..n]);

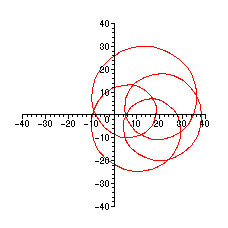
Nu ligger tydligen bara 2 nollställen inom cirkeln.

Vi får försöka med ett större r-värde.

Osv....

Efter en stunds prövande finner man att bland cirklar med tvådecimalsradier är den med r=2.15 den största som bara innehåller 3 nollställen.

Det är i det här fallet nödvändigt att förstora upp kurvan nära origo för att finna rätt r-värde. Eventuellt behöver man också fler plottningspunkter.
Försök i så fall med 'numpoints=200' inuti plot-kommandot.

Ex: plot([u,v,t=0..2*Pi],view=[-n..n,-n..n],numpoints=200) .