12.1. Konjugerade nollställen till reella polynom

Observera att satsen endast gäller för reella polynom.
Om någon koefficient a inte är reell gäller inte räkneregeln
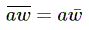
som används i beviset.
Notera också att om man multiplicerar ihop de faktorer i P(z), som svarar mot de komplexkonjugerade 0-ställena a+ib och a-ib, erhålles (z-a-ib)(z-a+ib) = (z-a)2 - (ib)2 = (z-a)2 + b2, dvs ett rent reellt uttryck av andra graden.
Detta visar att alla reella polynom i princip alltid kan faktoriseras i reella faktorer av högst andra graden.
Det uppstår dock ofta praktiska svårigheter att finna sådana faktoriseringar.