Advanced level courses at KTH and Stockholm University 2008-2009
Fall 2008
Integration theory
KTH, SF 2709, Serguei Shimorin
Course page (in Swedish)
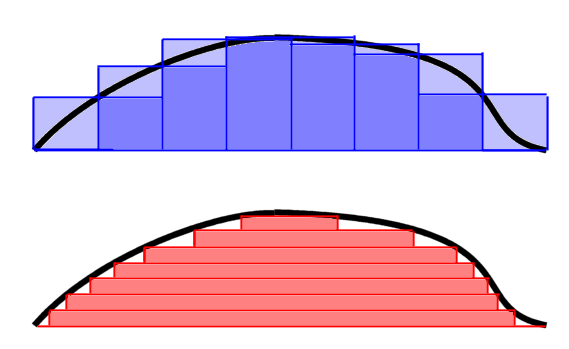
For all studies of analysis in higher mathematics it is fundamental
to understand the concept of integration. Our intuitive idea of the
integral of a function is as the area under its graph, and this can be
turned into a formal definition through approximating Riemann
sums. This leads to the Riemann integral which works fine in many
circumstances, but has its limitations.
One problem with the Riemann integral is that it does not manage
functions with too many discontinuities, for example the function f(x)
which is 1 if x is rational and 0 if x is irrational cannot be
integrated. Morally the integral should have the value zero since the
rationals form a countable set which should not contribute to the
integral. A more serious problem is that the Riemann integral does not
behave nicely when one studies sequences of functions, such as the
partial sums of a Fourier series approximating a periodic
function. When can one move the limit inside the integral?
In this course we will study the Lebesgue integral, and more
general concepts of integrals and measure. Among other things we will
see how the above problems are resolved and we will study the
important Lp spaces of functions.
The material in this course is fundamental also for the study of
probability theory.
Read more here:
Topics in mathematics III: Matrix groups
KTH, SF 2723, Mats Boij
Course page (in Swedish)
There exist many different natural sets of matrices that all have
the property that they are closed under multiplication and taking
inverses. Among them we find in particular the so-called classical
groups and you have certainly come across those in one form or
another, whether you realized it or not. They are the general linear
group Gln, the special linear group Sln, the
ortogonal group On, the special orthogonal group
SOn, and the symplectic group Spn.
During the course we will discuss a number of important concepts from
19th and 20th century mathematics that will help us to understand how
the classical groups look like. We will use methods from algebra,
topology, differential geometry and algebraic geometry. The idea is
that matrix groups, which themselves are of great interest in mathematics
and physics, will serve as a tool to understand the abstract concepts
that are needed to study them.
Read more here:
Chaotic dynamical systems
KTH, SF 2720, Michael Benedicks
Course page

For a number of years now, chaotic dynamical systems have received a lot of
scientific attention. One aspect is chaos, fractals, etc., often illustrated
with the fantastic pictures -- the Mandelbrot set, Julia sets, etc. -- that
computer simulations of iterations of complex polynomials give rise to.
Another aspect is formed by the so-called "strange attractors",
that occur in conjunction with computer simulations of ordinary
differential and difference equations. Some of the best known
mathematical experiments were carried out by the meteorologist
E. Lorenz and the astronomer M. Hénon, and here at the
department precisely these models have been studied rigorously and
chaotic behaviour was proved for them. D. Ruelle and
F. Takens have proposed that turbulent phenomena might at least
partially be explained via strange attractors.
The physicist M. Feigenbaum made the fundamental discovery
that many systems first go through a characteristic period doubling
and then behave in a random (chaotic) way, even though they are
deterministic. Later, one has shown that such period doublings occur
in liquid helium flow.
From a mathematical viewpoint, the course is quite special. On a
relatively elementary level, one obtains insight in phenomena that lie
quite close to current research. One or two computer experiments will
probably be part of the course. However, the course's main emphasis
will be on the mathematical theory, which in itself has a long history
with names such as Poincaré, Fatou, Birkhoff, and Smale, and which
lately has developed quickly, partly in symbiosis with computer
experiments.
Read more here:
Elementary differential geometry
SU, MM8010, Andrzej Szulkin
Course page (in Swedish)
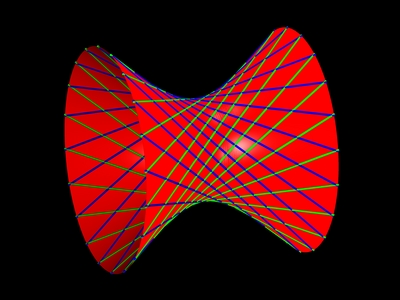
In this course we study curves and surfaces in three-dimensional
space. This subject has the beauty that one can start from knowing
only calculus of several variables, and reach many deep and
interesting facts.
The main new concept is that of curvature. In mathematics curvature
appears in many different forms, with the common property that it
measures how much an object differs from being flat. For example an
ordinary sphere has constant positive curvature, and the curvature
becomes larger as the radius is decreased. A linear plane has zero
curvature, but what would a surface of negative curvature be? Are
there closed surfaces of zero or negative curvature?
The most important result covered in the course is the Gauss-Bonnet
theorem. This relates the curvature of a surface to a topological
quantity (the Euler characteristic). This is a prototype of many
results in mathematics where geometry (which is computed locally, at a
microscopic level) is related to global topology (which can only be
seen by viewing the entire space).
Read more here:
(This course is followed by SF2722 Differential geometry at KTH.)
Algebra IV
SU, MM8004, Ralf Fröberg
Course page (in Swedish)
The course is a natural continuation of Algebra III at SU, where
groups, rings and fields are introduced. These notions are developed
further and new concepts are introduced as well. The material, which
in itself is abstract in nature, finds applications in several areas
of mathematics and is of fundamental importance in algebraic geometry
and algebraic topology. Topics include the tensor product, symmetric
and exterior algebras, chain conditions, modules, Jordan's normal
form, simple and semisimple algebras. (The course is quite similar,
but not identical, to SF2706 at KTH, which will not be given
2008/09.)
Read more here:
Analytic functions 2
SU, MM8007
Course page (in Swedish)
The course is a natural continuation of Analytic functions I at SU.
Some of the topics treated are: power series, analytic functions as
conformal maps, Möbius transformations with applications, elliptic
functions, modular forms, Cauchy's integral formula and the Cauchy
integral theorem with applications, the argument principle, and the
Riemann mapping theorem or the Dirichlet problem.
Read more here:
Spring 2009
Topology
KTH, SF 2721, Björn Gustafsson
Room 3733 (KTH), Tuesdays at 13-15. Course start: January 27
Course page (in Swedish)

Topology is the study of spaces from an abstract viewpoint. One is
interested both in the fine structure of a space and in global
features such as the number of holes. A fundamental concept is that of
a continuous function, or continuous map, and the goal is to
understand what properties such a map can have without using ideas
like distance or derivative.
For instance, it might seem obvious that a simple closed curve in
the plane divides the plane into an "inside" and an "outside"
region. This observation is correct, but to really prove it assuming
only that the curve is continuous is not an easy task. In fact, this
was a hard problem for a long time, studied by many mathematicians in
the 19th century. In the course we will see a proof of this "Jordan
curve theorem", and other results such as the "Ham sandwich theorem"
(one can always divide a three layer sandwich into two equal pieces
with just one cut) and the "Hairy ball theorem" (one cannot comb a
hedgehog).
A classical example in topology is that, in a world of perfect
rubber, a coffee cup cannot be distinguished from a doughnut, but is
fundamentally different from a ball. What does this observation mean?
And how can one turn it into computable mathematics? The answer,
perhaps surprisingly, involves group theory and abstract algebra. In
the course we will see how to find and classify all two-dimensional
surfaces. The doughnut and the ball are two of them.
Read more here:
Topics in mathematics IV: Prime numbers
KTH, SF 2724, Anders Karlsson
Room 3733 (KTH), Thurdays at 10-12. Course start: January 22
Course page (in Swedish)

Everybody knows what a prime number is and that there are
infinitely many of them; this course will go further. Some of the
topics that will be discussed: the prime number theorem (how the
number of prime numbers less than x grows with x); famous unsolved
problems (such as the Riemann hypothesis, the Goldbach conjecture, and
whether there are infinitely many prime twins) and results related to
these; a discussion of the abc conjecture, how it implies Fermat's
last theorem (proved by Andrew Wiles in 1994), and a quick proof of
the polynomial version of the conjecture; famous solved problems, such
as Dirichlet's theorem and a discussion of the recent theorem of Green
and Tao (both results deal with prime numbers in arithmetic
progressions). The proof of the prime number theorem requires some
complex analysis, but the rest of the material is largely
elementary. The course will provide an opportunity to learn about
fundamental results and open questions regarding prime numbers and to
appreciate the beauty and unity of mathematics.
Read more here:
Differential geometry
KTH, SF 2722, Mattias Dahl
Room 3733 (KTH), Tuesdays at 10-12. Course start: January 27
Course page (in Swedish)
In this course, differential geometry is developed from an abstract
viewpoint. The central objects of study are differentiable manifolds,
which are higher-dimensional generalizations of curves and surfaces,
without the restriction of being embedded in some Rn. The
essential idea is to study analysis in a coordinate-free fashion. The
derivative of a smooth map is "the best linear approximation" at a
point, and in calculus one has seen how to compute it as a matrix of
partial derivatives. But what does this mean if we have no particular
coordinates in which to compute partial derivatives?
Along the way we will see proper definitions of things like vector
and tensor fields, and we will see how to formulate and prove results
from vector analysis in a general setting. This coordinate-free
machinery is fundamental for many physical theories such as classical
mechanics and general relativity.
A manifold has a local structure which allows us to do analysis,
but on a global scale it can have interesting topological features. We
will see how analysis and topology come together in the notion of the
degree of a smooth map and also in Morse theory.
The concept of curvature appears when one introduces a Riemannian
metric on a manifold. In the course we will see how to define
distances, covariant derivatives, geodesics, and the curvature tensor,
and what they mean for the local geometry of a manifold.
Read more here:
(This course follows naturally "Elementary differential geometry"
at Stockholm University, and it is recommended to have taken this
course. A good knowledge of calculus of several variables and the
inverse and implicit function theorems is an important
prerequisite.)
Topics in mathematics V:
Clifford algebras, geometric algebra, and applications
KTH, SF 2725, Lars Svensson and Douglas Lundholm
Room 3721 (KTH), Thurdays at 15-17. Course start: January 29
Course page (in Swedish)
It is well known that the complex numbers form a powerful tool in
the description of plane geometry. The geometry of 3-dimensional space
is traditionally described with the help of the scalar product and the
cross product. However, already before these concepts were
established, Hamilton had discovered the quaternions, an algebraic
system with three imaginary units which makes it possible to deal
effectively with geometric transformations in three dimensions.
Clifford originally introduced the notion nowadays known as
Clifford algebra (but which he himself called geometric algebra) as a
generalization of the complex numbers to arbitrarily many imaginary
units. The conceptual framework for this was laid by Grassmann already
in 1844, but it is only now that one has fully begun to appreciate the
algebraisation of geometry in general that the constructions of
Clifford and Grassmann result in. Among other things, one obtains an
algebraic description of geometric operations in vector spaces such as
orthogonal complements, intersections, and sums of subspaces, which
gives a way of proving geometric theorems that lies closer to the
classical synthetic method of proof than for example Descartes's
coordinate geometry. This formalism gives in addition a natural
language for the formulation of classical physics and mechanics.
The best known application of Clifford algebras is probably the
"classical" theory of orthogonal maps and spinors which is used
intensively in modern theoretical physics and differential
geometry.
This course will run as a graduate course, but it will also be
possible to take it as an advanced level course.
Read more here:
Elementary algebraic geometry
SU, MM8013
Room 306 (SU), Mondays at 13-15. Course start: January 19
Course page (in Swedish)
.png)
Algebraic geometry is the study of the solutions of systems of
polynomial equations. Due to the special form of the equations, the
solution spaces, called algebraic varieties, are not as 'flexible' as
for example differentiable manifolds, but they carry a lot of
structure. For example, deep results have been obtained that relate
the solution spaces of the `same' system of equations over different
ground fields to each other.
This course introduces basic algebro-geometric notions such as
affine and projective algebraic varieties, dimension, nonsingularity,
and maps between algebraic varieties. Several concrete examples, such
as algebraic curves and surfaces, will be discussed as well.
Read more here:
Galois theory
SU, MM8005
Room 306 (SU), Thurdays at 13-15. Course start: January 22
Course page (in Swedish)

Galois theory is a beautiful and fundamental part of algebra
dealing with field extensions and field automorphisms. The main
theorem gives a 1-1 correspondence between the subextensions of a
given field extension satisfying certain properties and the subgroups
of a group of automorphisms associated to the extension.
Galois theory has many applications. Some of the best known
applications are the proof of the impossibility of the trisection of a
general angle with ruler and compass only and the proof that the
solutions of a general algebraic equation of degree five or higher
cannot be given only in terms of n-th roots and the basic algebraic
operations.
Read more here:
Mathematical and computational methods from micro to macro scales
KTH, Anders Szepessy
Room 4523 (KTH), Tuesdays at 10-12. Course start: January 27
Course page
Optimal control
KTH, SF2852, Ulf Jönsson
Room D34 (KTH), Wednesdays at 10-12. Course start: January 14
Course page (in Swedish)
Fördjupning i finansmatematik, fdk
SU, Thomas Höglund, Joanna Tyrcha
Room 14 (SU), Tuesdays and Fridays at 9-12. Course start: January 20
Course page
Analys av kategoridata, pk
SU, Juni Palmgren, Jan-Olov Persson
Room 32 (SU), Misc. days. Course start: March 23
Course page
Statistiska modeller, fdk
SU, Rolf Sundberg
Room 32 (SU), Tuesdays and Fridays at 9-12. Course start: March 24
Course page
|
|