Also known as the Serret-Frenet formulas, these vector differential equations relate inherent properties of a parametrized curve. In matrix form, they can be written
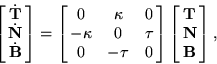
where T is the unit tangent vector,
N is the unit normal vector,
B is the unit binormal
vector, 
is the torsion, 
is the curvature, and 
denotes 
.
Centrode, Fundamental
Theorem of Space Curves, Natural
Equation
Frenet, F. "Sur les courbes à double courbure." Thèse. Toulouse, 1847. Abstract in J. de Math. 17, 1852.
Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, p. 186, 1997.
Kreyszig, E. "Formulae of Frenet." §15 in Differential Geometry. New York: Dover, pp. 40-43, 1991.
Serret, J. A. "Sur quelques formules relatives à la théorie des courbes à double courbure." J. de Math. 16, 1851.
 | |||
|
 |
| |