The line integral of a vector field ![]() on a curve
on a curve ![]() is defined by
is defined by
| (1) |
where ![]() denotes a dot product. In
Cartesian coordinates, the line integral can be written
denotes a dot product. In
Cartesian coordinates, the line integral can be written
| (2) |
where
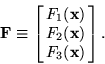 |
(3) |
For z complex and
![]() a path in the complex plane
parameterized by
a path in the complex plane
parameterized by ![]() ,
,
| (4) |
Poincaré's
theorem states that if ![]() in
a simply connected neighborhood
in
a simply connected neighborhood ![]() of
a point x, then in this neighborhood, F is the gradient of a scalar field
of
a point x, then in this neighborhood, F is the gradient of a scalar field
![]() ,
,
| (5) |
for ![]() ,
,![]() is
the gradient operator. Consequently, the gradient
theorem gives
is
the gradient operator. Consequently, the gradient
theorem gives
| (6) |
for any path ![]() located completely within
located completely within ![]() ,
,![]() and
ending at
and
ending at ![]() .
.
This means that if ![]() (i.e.,
(i.e., ![]() is an irrotational
field in some region), then the line integral is path-independent in
this region. If desired, a Cartesian path can therefore be chosen between
starting and ending point to give
is an irrotational
field in some region), then the line integral is path-independent in
this region. If desired, a Cartesian path can therefore be chosen between
starting and ending point to give
| (7) |
If ![]() (i.e.,
(i.e., ![]() is
a divergenceless
field, a.k.a. solenoidal
field), then there exists a vector field
A such that
is
a divergenceless
field, a.k.a. solenoidal
field), then there exists a vector field
A such that
| (8) |
where A is uniquely determined up to a gradient field (and which
can be chosen so that ![]() ).
).
![]() Conservative
Field, Contour
Integral, Gradient
Theorem, Irrotational
Field, Path
Integral, Poincaré's
Theorem
Conservative
Field, Contour
Integral, Gradient
Theorem, Irrotational
Field, Path
Integral, Poincaré's
Theorem
![]()
![]()
Krantz, S. G. "The Complex Line Integral." §2.1.6 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 22, 1999.
![]()
![]()

|
 |

| |