P3.1c.1 Gränsvärden, förkortning/insättning.
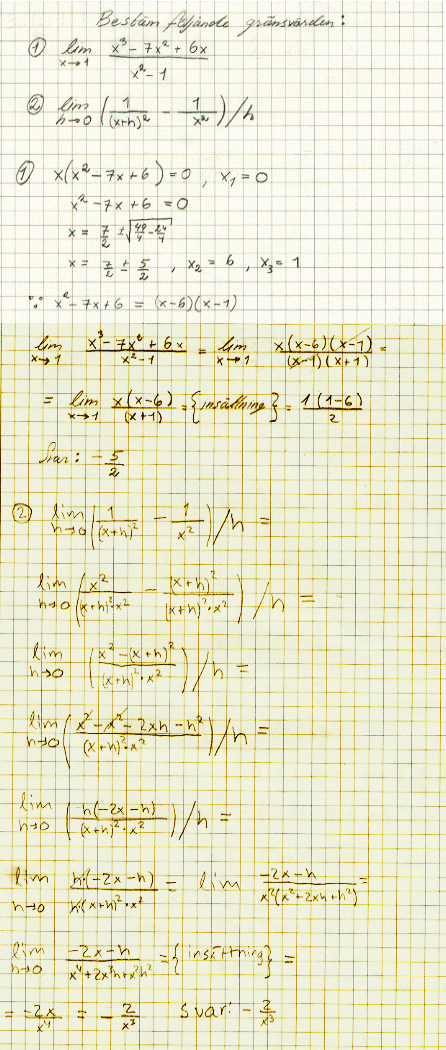
1.Typ: förkortning/insättning.
OBS! x finns i varje term i täljaren. Bryt ut x.
Faktorisera täljaren genom att bestämma alla nollställen.
Man kan undersöka om det faktoriserade uttrycket stämmer.
Efter förkortning av (x-1) blir inte nämnaren 0 då man sätter in x=1. Alltså är insättning OK!
(L'Hospital kan också användas, dock jobbigt i detta fall Inte så farligt!/GJ)
2. Typ: förkortning/insättning.
Sätt på gemensamt bråkstreck.
OBS! kancellation!
Bryt ut h.
Sätt in h i parentesen. OBS! h hamnar i nämnaren.
h tar ut varandra.
Nu blir inte nämnaren 0, alltså är insättning OK!
Derivatans definition:f '(a) = lim(h->0) ( f(a+h)-f(a) )/h
I detta fall är f(x)= 1/(x^2). Notera: Derivatan av 1/(x^2) är -2/(x^3).