1.4.Planets ekvation
Notera hur man använder skalärproduktens egenskap att vara = 0 då vektorerna är vinkelräta.
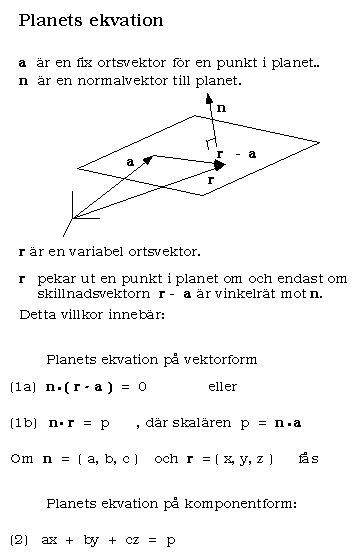
r betraktas som en variabel vektor, r = (x, y, z), som skall uppfylla det angivna skalärproduktsvillkoret för att vara en ortsvektor för en punkt i planet.
Som för den räta linjen behövs det två vektorer för att
karakterisera ett plan:
En ortsvektor a för en punkt i planet och en normalvektor n
vinkelrät mot planet.
Observera hur enkelt det är att ta fram normalvektorn n ur planets ekvation på komponentform!
Besvarade frågor länkas från denna sida, samt förstasidan.