2.4 Kurva och tangent.

Här nedan är Taylorutvecklingen av en R ->R³ - funktion,
dvs. en funktion som geometriskt representeras av en kurva i 3-dimensionella rummet.

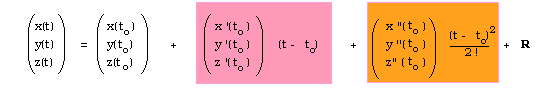
Man Taylor-utvecklar de tre envariabelfunktionerna x(t), y(t) och z(t) separat och sätter in resultaten i en 3-dimensionell vektor.

Den linjära delen är märkt rosa och den kvadratiska orange.

Den linjära och den konstanta delen utgör ekvationen för en rät linje, kurvans tangentlinje, i punkten
( x(t_o), y(t_o), z(t_o) ).

Jämför med linjens allmänna ekvation:

(1)     r = a +tv eller (då man vill att punkten med ortsvektorn a skall svara mot t = t_o )

(2)      r = a + (t-t_o)v.

Man ser att a svarar mot punkten (x(t_o), y(t_o), z(t_o) och att tangentlinjens riktningsvektor är:

v = (x'(t_o), y'(t_o), z'(t_o) ).

Resonemanget bygger på att att kurvfunktionerna är deriverbara för t = t_o.

För att man skall förstå kopplingen till vektoralgebran måste man känna igen vektorerna i linjens ekvation i Taylorutvecklingens kolumnvektorer.
Dessutom måste man se att parentesen (t-t_o) i linjens ekvation (2) garanterar att t=t_o svara mot r = a.