4.1 Linjära och olinjära transformationer.
Här undersöks speciellt den olinjära koordinattransformationen
u=x2 - y2, v = 2xy.
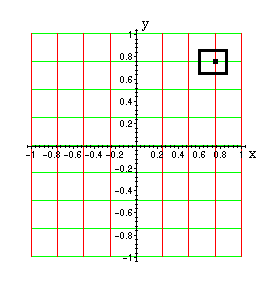
Här visas hur rutmönstret nedan till vänster avbildas.
Man kan visa att den givna transformationen avbildar både vågräta och lodräta linjer på liggande
parabler.
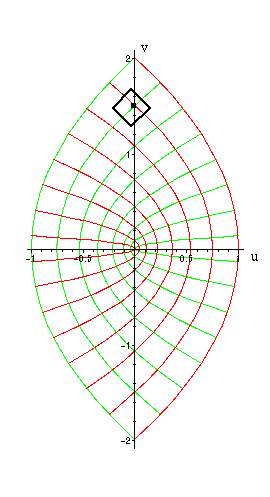
Därför blir bilden av rutmönstret ett system av parabler nedan till höger.
|
|
Transformationens Jacobimatris är:
 , i punkten (0.75,0.75) :
, i punkten (0.75,0.75) :
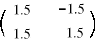
Den konstanta Jacobimatrisen i punkten definierar en linjär transformation.
För linjära transformationer gäller att linjer avbildas på linjer.
Här ser man hur rutmönstret ovan till vänster avbildas av den linjära transformation som definieras av
Jacobimatrisen i punkten (0.75, 0.75).

Observera färgerna. Gröna linjer avbildas på gröna parabler osv.
Den utmärkta punkten (0.75 , 0.75) med den rektangulära omgivningen avbildas på motsvarande utmärkta objekt till höger.
Man kan jämföra bilden av Jacobimatrisens linjära transformation med den olinjära transformationens avbildning av det inramade området omkring punkten (0.75, 0.75).
Om man tänker sig att den inramade delen av övre bilden flyttas så att bildpunkten läggs i origo i undre bilden kan man se att den linjära transformationens bildlinjer tangerar den olinjära transformationens bildkurvor i origo.
Man kan också säga att Jacobimatrisen i punkten definierar den linjära transformation som bäst approximerar den olinjära koordinattransformationen i punkten.
Jämför relationen mellan en kurva osh dess tangentlinje resp. en yta och dess tangentplan i en punkt.
MAII 4.5.2 och 4.7.
Besvarade frågor länkas från denna sida, samt förstasidan.