2A.2.1. Flervariabelgränsvärde
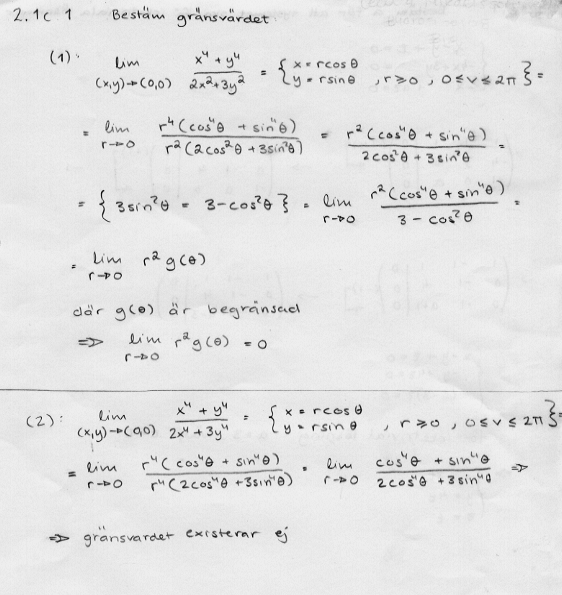
(1) Flervariabelgränsvärdet ska bestämmas.
För att göra detta användes polära koordinater så att det blir ett envariabel- gränsvärde att lösa.
Till slut så fås ett uttryck där r2 är multiplicerat med en begränsad funktion, eftersom nämnaren aldrig kan bli noll.
Därför blir gränsvärdet = 0 oberoende av vägen till origo.
Flervariabelgränsvärdet existerar alltså.
(2) Gör på samma sätt som i första exemplet.
Här kommer r i täljare och nämnare att ta ut varandra.
Då får man ett gränsvärde där r->0 av en funktion som enbart beror av vinkeln. Man får något som kallas spiraltrappsdiskontinuitet.
Gränsvärdet existerar inte.