P3.3c.1 Bestämning av inversmatris med hjälp av adjunkten
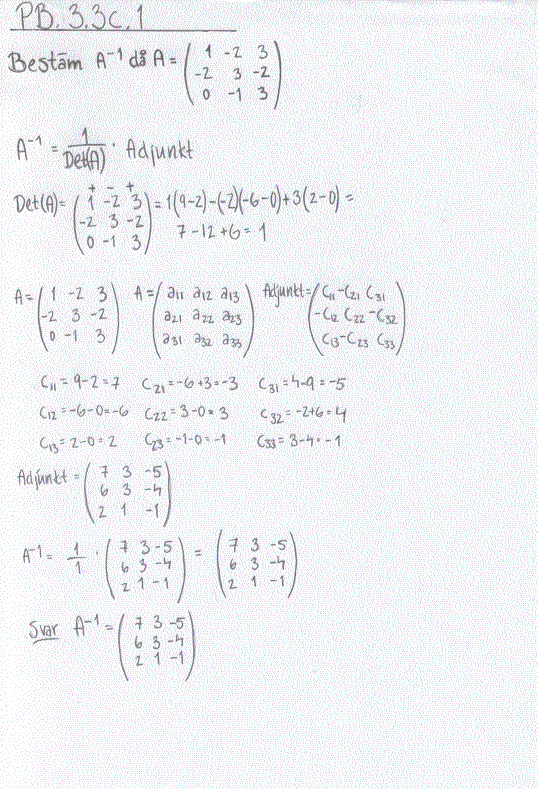
Vi har lärt oss två sätt att bestämma A:s invers A-1:
1.[ A | E ] omvandlas med Gauss-Jordan till [E | A-1]
2.A-1 = (1/Det(A)) * Adjunkt.
Här visas 2.
A-1 existerar endast om Det(A) ≠ 0.
A innehåller minorer ( eller cofactorer) Cij. Varje minor räknas ut genom vanlig kryssning i A. Man får till exempel C21 genom att kryssa i A utifrån a21 *). Adjunktens komponenter får man fram genom att byta ordningen på placeringssiffrorna i Cijoch lägga till (-) framför varannan minor.. Detta betyder att Adj21 blir -C12 och Adj13 blir C31 **)
Du kan kontrollera om du räknat rätt. Detta görs genom att kolla att A*A-1= E. Kontrollera själv och se det som övning i matrismultiplikation.
*) För att få C21 stryker man alltså rad 2 och kolumn 1 i A och räknar ut determinanten för den kvarvarande matrisen.
**) Man kan också uttrycka det så att Adjij = (-1)i+jCji
GJ