4C.2.1 Differentialräkning.
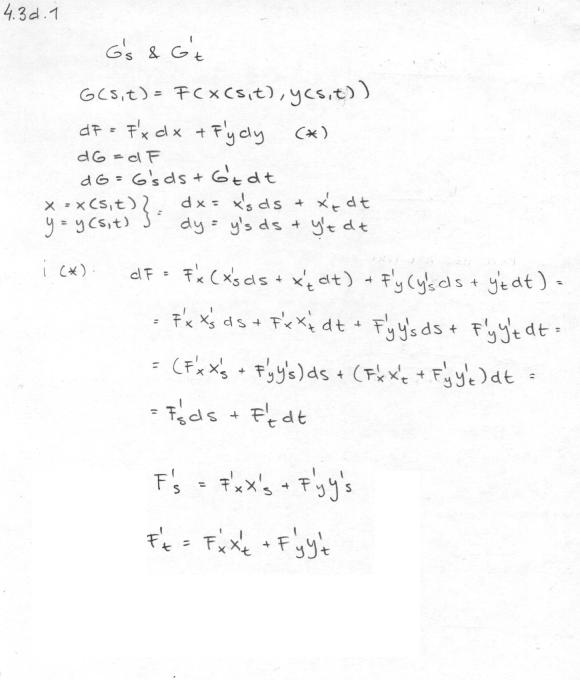
G är alltså en sammansatt funktion vars derivator G's och G't skall beräknas med hjälp av differentialer (annars går det bra med kedjeregeln också).
Knepet är att man kan bilda differentialer av de inre funktionerna också:
dx = ...
dy= ...
som kan sättas in i
dF =F'xdx + F'ydy.
Till slut får man två versioner av differentialen dF.
Där får man de sökta sambanden genom identifiering.
Man sätter alltså koefficienterna för ds och dt lika med varandra.
/GJ