4D.1.2 Existens av differentierbar invers av R2-R2-funktion
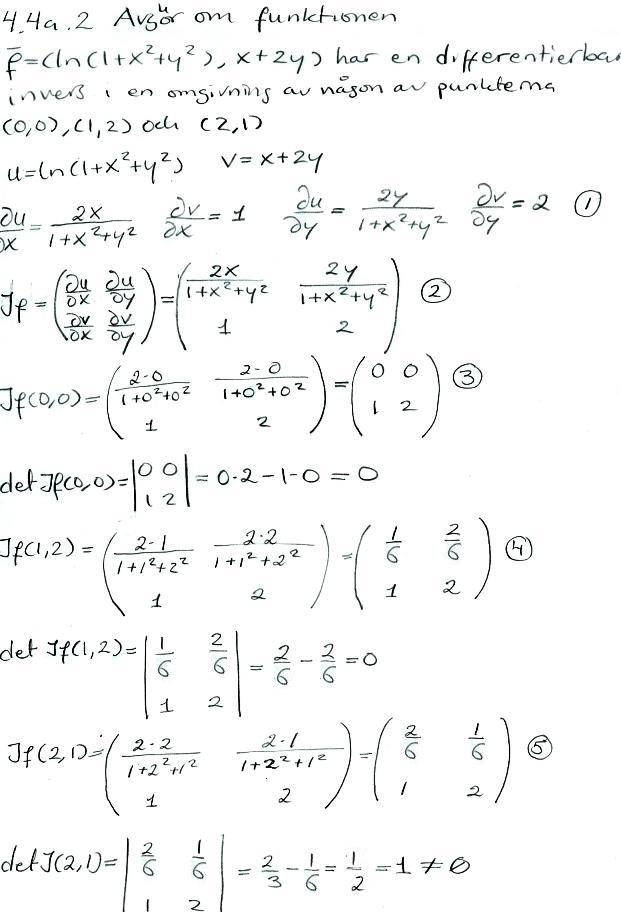
2. Skapar en jacobimatris
3. Stoppar in punkten (0,0) i Jacobimatrisen och räknar därefter dess determinant.
4. Jag stoppar nu istället in punkten (1,2) i Jacobimatrisen och räknar dess determinant.
5. Jag stoppar nu istället in punkten (2,1) i Jacobimatrisen och räknar dess determinant.
Funktionen är inverterbar lokalt precis när dess Jacobimatris är inverterbar, och denna Jacobimatris är i sin tur inverterbar precis när dess determinant är skild från noll. Således har funktionen en differentierbar invers i en omgivning av (2,1) men inte (0,0) och (1,2)
K-04