5B.3.2 Egenvärden och ortogonala egenvektorer för symmetrisk matris.
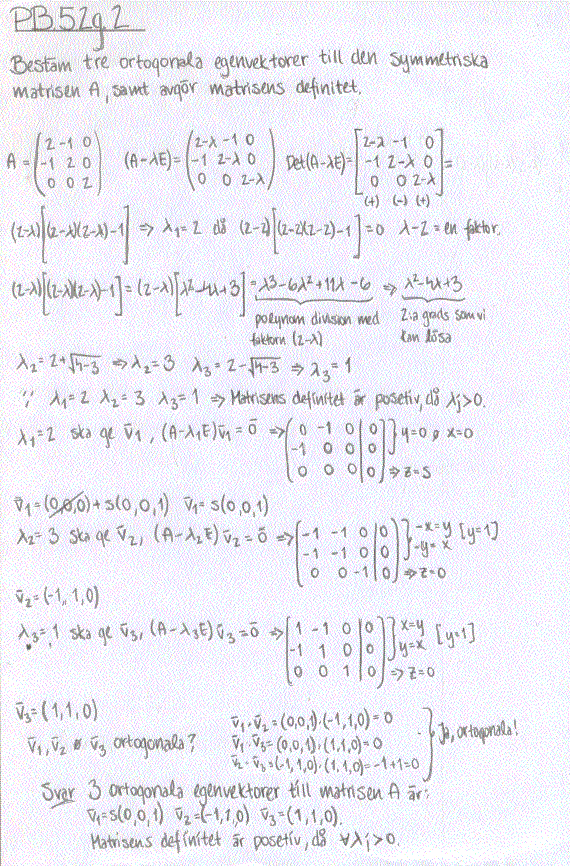
Vi ska ta fram ortogonala egenvektorer , dvs skalärprodukterna av egenvektorerna v1 v2 och v3 (parvis) ska bli 0.

Att matrisen är symmetrisk innebär att
  1. A`s egenvärden är reella.
  2. Det är möjligt att få fram ortogonala egenvektorer!
  3. Vi kan alltid ta fram en ON-matris (o=ortogonal n=normaliserad) som diagonaliserar den.
Definitheten av matrisen avgörs av egenvärdenas tecken.
  1. alla egenvärden större än 0 = positivt definit .
  2. de olika egenvärdena har olika tecken = indefinit.
  3. alla egenvärden är mindre än 0 = negativt definit
Egenvärdena:
Vi ser att det är enklast att utveckla determinanten längs den nedre raden,

Egenvektorerna v1 v2 och v3 erhålls genom (A-lambdaE)v=0, där de olika egenvärdena sätts in.
Systemet ger egenvektorerna som lösningar.
Sist så kollar vi om egenvektorerna är ortogonala genom att kolla skalärprodukten mellan dem.
Nyckelord: symmetrisk matris, egenvärde, egenvektor, ortogonal, definit HE