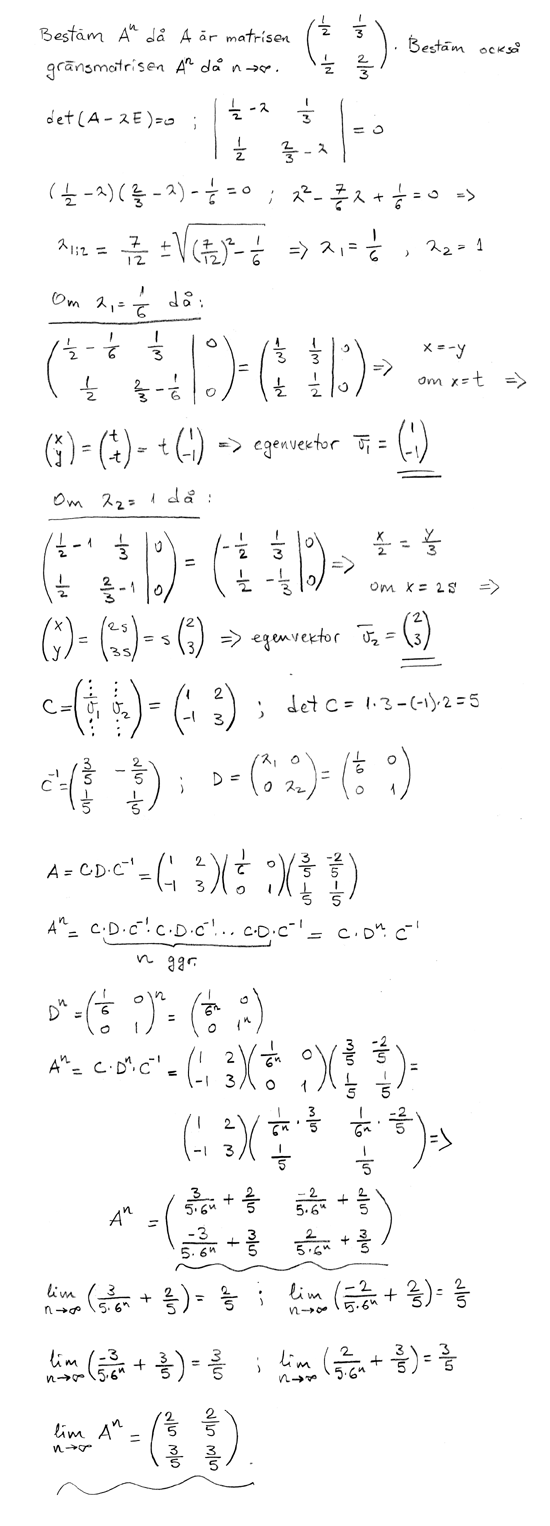
Den karakteristiska ekvationen.

Egenvärden.

  Egenvektorer bildar transformationsmatrisen C.

Observera kancellationerna C^-1·C· osv.  

Man lägger märke till att kolumnsummorna för A, A² osv. är 1 och att komponenterna ligger mellan 0 och 1.
Sådana matriser används för att definiera Markov-kedjor,
v, Av, A²v, A³v ... bildat av s.k. tillståndsvektorer vars komponenter kan tolkas som sannolikheten för ett visst tillstånd.

Matriserna Aⁿ konvergerar under allmänna villkor till en gränsmatris med identiska kolumner som är lika med A:s (ofta unika) egenvektor svarande mot egenvärdet 1. Kolumnvektorerna/egenvektorerna normeras så att kolumnsumman blir 1. Notera vad egenvektorn v₂ i detta exempel blir om den normeras till kolumnsumman = 1!
/GJ