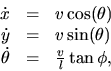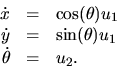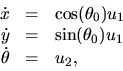Example:
Car steering
The steering system of a car can be modeled as
|
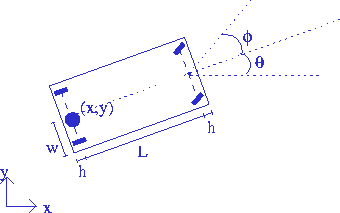
Figure 1:
The geometry of the car-like robot, with position (x,y),
orientation |
|
|
|
|
|
|
|
(1) |
where
x and y are cartesian coordinates of the middle point on the rear
axle, ![]() is
the orientation angle, v is the longitudinal velocity measured at that
point, l is the distance of the two axles, and f is the steering angle. In this case v and f are the two controls.
is
the orientation angle, v is the longitudinal velocity measured at that
point, l is the distance of the two axles, and f is the steering angle. In this case v and f are the two controls.
Let us reduce the complexity by defining u1=v, u2=v/l tan f, then
|
|
|
(2) |
Sometimes, this is called a unicycle model. If we linearize (2) around a point (x0, y0,q0), we have
|
|
|
(3) |
which is not controllable. However, using geometric tools we will show in Chapter 8 that the nonlinear system (2) is controllable (This is what you, as a driver, expected, right?).


 <>
<>