Ingemar Nåsell och Hans Thunberg,

Kursen 5B1212 i differentialekvationer och transformer, höstterminen 2004, Matematik, KTH.

Maple och Ordinära Differentialekvationer

I detta arbetsblad för Maple finns en kortfattad beskrivning av några Maple-kommandon som är användbara när man studerar ordinära differentialekvationer. Vi påminner om att det finns mycket information om Maple i dess on-line help.

1. Ordinära differentialekvationer med symbolisk lösning

Om man vill bestämma derivatan av en funktion y(x) så skriver man så här:

>	diff(y(x),x);

Andraderivatan av samma funktion fås med följande kommando:

>	diff(y(x),x$2);

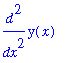
Om y(x) är ett explicit uttryck så beräknas dess derivata:

>	diff(sin(x^2),x);

>	diff(sin(x^2),x$2);

Ibland kan man hitta explicita lösningar till ordinära differentialekvationer. Maple har ett kommando, dsolve, för att söka sådana lösningar. Vi visar först hur detta fungerar på en linjär differentialekvation. Kommandot dsolve används med två argument, varav det första är den ekvation som skall lösas, och det andra är namnet på lösningen. Observera att man måste skriva y(x) i stället för y överallt i ekvationen där y förekommer.

>	dsolve(diff(y(x),x)+2*y(x)=x, y(x));

Om vi vill lösa det motsvarande initialvärdesproblemet så måste vi informera Maple om både ekvationen och initialvärdet. Bägge av dem ges som en mängd (innanför krullparenteser) som utgör det första argumentet till kommandot dsolve:

>	dsolve({diff(y(x),x)+2*y(x)=x, y(0)=y0}, y(x));

Ett exempel till:

>	dsolve(diff(y(x),x$2)-y(x)=x^2, y(x));

Eftersom detta är en ekvation av ordningen två så innehåller den allmänna lösningen två godtyckliga konstanter. Alternativt kan vi bestämma lösningen till diffekvationen med givna initialvärden på y och dess derivata. Notera att villkoret på första derivatan skrives D(y)(0)=1.

>	dsolve({diff(y(x),x$2)-y(x)=x^2, y(0)=0, D(y)(0)=1}, y(x));

I nästa exempel använder vi tekniken att lagra differentialekvationen i en variabel med namnet ekv1:

>	ekv1:=diff(y(x),x)=1/((y(x)-1)*(y(x)-2)*(y(x)-3));

Nu kan vi använda detta namn på ekvationen när vi anropar dsolve:

>	dsolve(ekv1, y(x));

Här fick vi inte mindre än fyra funktioner som alla tydligen satisfierar den givna differentialekvationen. Men vårt grundläggande resultat om existens och entydighet säger att vi väntar oss en entydig lösning om det givna uttrycket för derivatan är kontinuerligt, liksom dess partiella derivata med avseende på y, och ett initialvärde är specificerat. Vilken lösning skall vi välja om y(0)=0? Maple ger svaret:  

>	dsolve({ekv1,y(0)=0}, y(x));

Den givna ekvationen är singulär för y-värdena 1, 2 och 3. Man kan därför förvänta sig olika beteenden för lösningskurvorna

för initialvärden y(0) i de två intervallen (1,2) och (2,3) samt för y(0)>3. Vi ser på dem i tur och ordning och ger namn åt dem.

>	dsolve({ekv1,y(0)=1.5}, y(x));

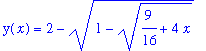
>	dsolve({ekv1,y(0)=2.5}, y(x));

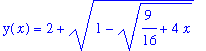
>	dsolve({ekv1,y(0)=4}, y(x));

De första och sista av dessa fyra lösningar existerar för x > -9/4, medan lösningarna nr 2 och nr 3 existerar på det begränsade x-intervallet -9/64 < x < 7/64. Dessa villkor får man genom att kräva att de storheter som man drar kvadratrötter ur skall vara positiva. Hur beter sig dessa olika lösningar när x närmar sig begränsningarna av existens-intervallen? Försök att svara på denna fråga genom att se på den givna differentialekvationen. Både de explicita lösningarna ovan och differentialekvationen visar att derivatan har konstant tecken så länge som den är kontinuerlig, d.v.s. så länge som lösningen existerar. Vi återkommer och ritar alla fyra lösningskurvorna i Avsnitt 3 härnedan.    

2. Plottning av riktningsfält och lösningskurvor

Kommandot DEplot används för att plotta både riktningsfält och specifika lösningskurvor. Detta kommando ligger i paketet DEtools och läses in i minnet på följande sätt:

>	with(DEtools,DEplot);

Kommandot DEplot används med följande fem argument:  1) Differentialekvationen, 2) Namn på den sökta lösningen, 3) Intervall för den oberoende variabeln, 4) Intervall för den beroende variablen, 5) En lista av listor med initialvillkor. Notera att en lista i Maple ges mellan hakparenteser. Om man utelämnar det femte kommandot så plottas bara riktningsfältet. Vi börjar med att undersöka ekvationen ekv2 definierad på nästa rad. Observera att vi har löst den ovan.

>	ekv2:=diff(y(x),x)-y(x)=x^2;

Hur ser riktningsfältet ut?

>	DEplot(ekv2, y(x), x=-2..2, y=-2..2);

Vi plottar också några lösningskurvor. För att få tydliga kurvor i utskriften ber vi om svarta kurvor med tjockleken 4.

>	DEplot(ekv2,y(x), x=-2..2, y=-2..2, [[y(0)=-1],[y(0)=0],[y(0)=1]], thickness=4, linecolor=black);

Det går också bra att undertrycka riktningsfältet. Det gör man genom att be att inga pilar ritas.

>	DEplot(ekv2,y(x), x=-2..2, y=-2..2, [[y(0)=-1],[y(0)=0],[y(0)=1]], arrows=NONE, thickness=4, linecolor=black);

Vi ser på ett till exempel:

>	ekv3:=diff(y(x),x)-y(x)=sin(2*x);

Riktningsfältet ser ut så här:

>	DEplot(ekv3,y(x), x=-2..2, y=-2..2);

Några lösningskurvor:

>	DEplot(ekv3, y(x), x=-2..2, y=-2..2, [[y(0)=-1], [y(0)=0], [y(0)=1]], arrows=NONE, thickness=4, linecolor=black);

3. Rita flera kurvor i samma figur

Ovan har vi ritat flera lösningskurvor i samma figur. Det kan emellertid hända att man behöver ange olika x-intervall för att numeriskt bestämma de olika lösningarna, och då kan man få problem med den metod som fungerade så bra härovan för lösningskurvorna till ekv3. Ett exempel ges av de fyra lösningarna till ekvationen ekv1. Vi använder nu metoden att lagra en hel plot i en s.k. plotstruktur. För att sedan rita denna plot nyttjar vi kommandot display. Detta finns i paketet plots och läses in i minnet med följande kommando:

>	with(plots,display);

Vi studerar nu de fyra lösningarna till ekv1 och definierar fyra plotstrukturer med namnen plot1, plot2, plot3, plot4. Notera att definitionen av plotstrukturen avslutas med ett kolon i stället för ett semikolon.

>	plot1:=DEplot(ekv1, y(x), x=-9/4..3, y=-0.5..1, [[y(0)=0]], arrows=NONE, thickness=4, linecolor=black): display(plot1);

Lösningskurvan har en knyck för x ungefär lika med -2. Detta beror på att vi har använt en för stor steglängd. Maple väljer själv steglängden till 1/20 av längden av x-intervallet. Vi kör om kommandot med en kortare steglängd:

>	plot1:=DEplot(ekv1, y(x), x=-9/4..3, y=-0.5..1, [[y(0)=0]], arrows=NONE, stepsize=0.1, thickness=4, linecolor=black): display(plot1);

Detta gav en klar förbättring. Vi fortsätter med att rita lösningskurvan motsvarande y(0)=1.5.

>	plot2:=DEplot(ekv1, y(x), x=-9/64..7/64, y=1..2, [[y(0)=1.5]], arrows=NONE, thickness=4, linecolor=black): display(plot2);

Den tredje lösningskurvan startar i y(0)=2.5:

>	plot3:=DEplot(ekv1, y(x), x=-9/64..7/64, y=2..3, [[y(0)=2.5]], arrows=NONE, thickness=4, linecolor=black): display(plot3);

Den fjärde lösningskurvan startar i y(0)=4:

>	plot4:=DEplot(ekv1, y(x), x=-9/4..3, y=3..5, [[y(0)=4]], arrows=NONE, stepsize=0.1, thickness=4, linecolor=black): display(plot4);

Vi ritar alla fyra lösningskurvorna i samma figur så här: Observera att argumentet till kommandot display är en mängd av plotstrukturer, med mängdelementen inneslutna av en krullparentes.

>	display({plot1,plot2,plot3,plot4});

4. Fasporträtt för ett system av autonoma differentialekvationer av första ordningen

Fasporträtt ritas med hjälp av kommandot DEplot. Kom ihåg att detta kommando ligger i paketet DEtools och att det måste läsas in i minnet så här:

>	with(DEtools,DEplot);

Vi ser på ett exempel. Vi börjar med att definiera och ge namn åt de två differentialekvationerna:

>	eq1:=diff(x(t),t)=2*sin(y(t)^3); eq2:=diff(y(t),t)=-sin(x(t)^3);

Hur ser vektorfältet ut?

>	DEplot([eq1,eq2], [x,y], t=0..10, x=-2..2, y=-2..2);

Rita några banor med följande initialvärden:

>	inits:=[[x(0)=1,y(0)=0],[x(0)=2,y(0)=0],[x(0)=0,y(0)=2]];

>	DEplot([eq1,eq2], [x,y], t=0..10, x=-2..2, y=-2..2, inits, stepsize=0.1, thickness=4, linecolor=black);

De tre initialpunkterna synes alla leda till slutna banor.

Vi studerar ett till exempel, taget från Zill och Cullen 8.2:36.

>	eq3:=diff(x(t),t) = 4*x(t)+5*y(t); eq4:=diff(y(t),t) = -2*x(t)+6*y(t);

>	DEplot([eq3,eq4], [x,y], t=0..1, x=-1..1, y=-1..1);

Origo är här en instabil spiralpunkt. Banorna rör sig medsols runt origo. Vi plottar ett par banor med följande initialvärden:

>	inits:=[[x(0)=0.1,y(0)=0],[x(0)=0,y(0)=-0.1],[x(0)=-0.1,y(0)=0],[x(0)=0,y(0)=0.1]];

>	DEplot([eq3,eq4], [x,y], t=0..1, x=-1..1, y=-1..1, inits, thickness=4, linecolor=black);

>