The term ``geometric'' suggests several things. First it suggests that the setting is linear state space and the mathematics behind is primarily linear algebra (with a geometric flavor). Secondly it suggests that the underlying methodology is geometric. It treats many important system concepts, for example controllability, as geometric properties of the state space or its subspaces. These are the properties that are preserved under coordinate changes, for example, the so-called invariant or controlled invariant subspaces. On the other hand, we know that things like distance and shape do depend on the coordinate system one chooses. Using these concepts the geometric approach captures the essence of many analysis and synthesis problems and treat them in a coordinate-free fashion. By characterizing the solvability of a control problem as a verifiable property of some constructible subspace, calculation of the control law becomes much easier. In many cases, the geometric approach can convert what is usually a difficult nonlinear problem into a straight-forward linear one.
The linear geometric systems theory was extended to nonlinear systems in the 1970's and 1980's (see the book by Isidori). The underlying fundamental concepts are almost the same, but the mathematics is different. For nonlinear systems the tools from differential geometry are primarily used.
In the rest of the chapter, we use some typical problems and examples to illustrate the advantages and basic ideas of geometric approaches.
Let us start with an example of a linear system. The purpose of the example is to show that we can model even quite complex practical systems as linear systems.
Example: Longitudinal motions of an aircraft
By longitudinal motions of an aircraft we mean, the movement of an aircraft as if it were constrained to move exclusively in a vertical plane. This is a very important type of motion of an aircraft. It is possible to show that under perfect geometrical and dynamical symmetry conditions, the linearized equations of motion of any aircraft exhibit an exact longitudinal-lateral decoupling. The full explanation of the model equations falls outside the scope of this work, and can be found in (Etkin).
In our notations, V stands for the velocity modulus, m is the mass of the
aircraft, T is the thrust force exerted by the engines and supposed
to be acting along the main body axis, D is the magnitude of the
total aerodynamic drag acting opposite to the velocity vector, L is
the total aerodynamic magnitude of the lift force in an orthogonal
direction to the velocity, mg is the gravity force acting at the
center of gravity (CG) and pointing downwards (flat Earth
approximation). My is the total pitching moment around the axis
perpendicular to the plane of movement, ![]() is the angle of
attack of the aircraft (angle between the velocity and the x-axis),
is the angle of
attack of the aircraft (angle between the velocity and the x-axis),
![]() is the angle of climb (between the horizontal axis and the
velocity), and
is the angle of climb (between the horizontal axis and the
velocity), and ![]() is the pitch angle of the
aircraft. By convention, the pitch rate (
is the pitch angle of the
aircraft. By convention, the pitch rate (![]() in the
longitudinal motions) is denoted q.
in the
longitudinal motions) is denoted q.
The linearized equations of motion are:
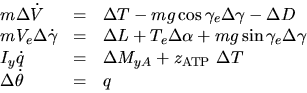 |
(1) |
| |
(2) |
Here are a few samples of the problems we will study in this course.
Problem: Disturbance decoupling
| |
(3) |
u=Fx+v
such that the output y is unaffected by the disturbance w.
Suppose such a feedback exists. Then by plugging in the control, we
have
| (4) |
y(n)(t)=C(A+BF)nx(t)+C(A+BF)n-1Bv(t)+C(A+BF)n-1Ew(t),
(here we assume v and w are constants for the sake of simplicity) we must have![]()
However, the equations are highly nonlinear, thus difficult to solve. In Chapter 3 we will use the idea of ``controlled invariance'' to reduce the problem into a linear one.
Problem: Output regulation
Consider
| (5) |
| (6) |
The difference with the disturbance decoupling problem is that here we only require the output to reject the disturbance in the steady state, and we also have some knowledge about the disturbance. The discussion of this problem in Chapter 7 will lead to the famous ``internal model principle'' (Wonham and Francis). Surprisingly we will show that this problem is generically solvable while the disturbance decoupling problem is not. Not surprisingly, the idea of controlled invariance also plays a central role here.
Problem: Controllability under constraints
| |
(7) |
u=Fx+Gv,
if we require that the trajectoryThis problem is quite relevant in many applications, for example, in path planning for mobile systems.
In this set of lecture notes, we will also discuss some system concepts for nonlinear systems. We give an example here to illustrate why sometimes one has to use nonlinear tools.
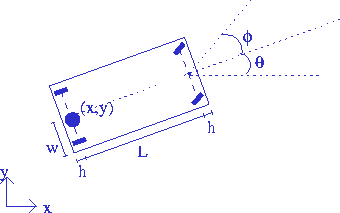
Example: Car steering
The steering system of a car can be modeled as
|
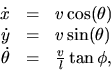 |
(8) |
Let us reduce the complexity by defining u1=v, ![]() , then
, then
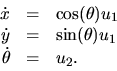 |
(9) |
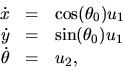 |
(10) |
The notes are organized as follows.
In Chapter 2, invariant and controlled invariant subspaces will be discussed; In Chapter 3, the disturbance decoupling problem will be introduced; In Chapter 4, we will introduce transmission zeros and their geometric interpretations; In Chapter 5, noninteracting control and tracking will be studied as applications of the zero dynamics normal form; In Chapter 6, we will discuss some input-output behaviors from a geometric point of view; In Chapter 7, we will discuss the output regulator problem in some detail. Finally, in Chapter 8, we will extend some of the central concepts in the geometric control to nonlinear systems.