Advanced level courses at KTH and Stockholm University 2009-2010
Fall 2009
Topics in Mathematics I: Graph Theory
KTH, SF 2704, Svante Linusson
Room 3721 (KTH), Tuesdays at 10-12. Course start: September 1
Course page
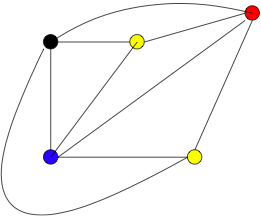
A graph consists of a set of vertices and a set of edges connecting pairs of vertices. A graph is often drawn with a dot for each vertex and a line connecting two dots for every edge.
Graphs can be used to model very different situations; roads connecting cities, wires connecting computers, friendship connecting people, or much more abstract mathematical situations.
During the first part of the 20th century much of graph theory was inspired by the famous four-color conjecture. It says that the vertices of any planar graph (i.e. a graph that may drawn in the plane with no crossing edges) can be colored with only 4 colors such that no vertices sharing an edge get the same color.
This was proved (with computer assistance) in 1976. The explosive growth of graph theory in recent years is largely due to its use as the structure underpinning modern applied mathematics (computer science, combinatorial optimization etc.). The purely mathematical questions in graph theory are often very interesting in themselves. Questions may be very easy to ask but very difficult to answer. Examples of questions one may ask are: How many colors are needed for a particular graph?, when are two graphs isomorphic? (i.e. the same graph but presented differently), how well connected is the graph? Does a given graph contain a certain substructure or not?
Read more here:
Integration Theory
KTH, SF 2709, Serguei Shimorin
Course page
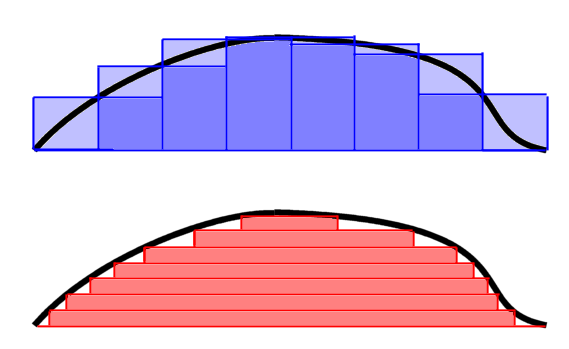
For all studies of analysis in higher mathematics it is fundamental
to understand the concept of integration. Our intuitive idea of the
integral of a function is as the area under its graph, and this can be
turned into a formal definition through approximating Riemann
sums. This leads to the Riemann integral which works fine in many
circumstances, but has its limitations.
One problem with the Riemann integral is that it does not manage
functions with too many discontinuities, for example the function f(x)
which is 1 if x is rational and 0 if x is irrational cannot be
integrated. Morally the integral should have the value zero since the
rationals form a countable set which should not contribute to the
integral. A more serious problem is that the Riemann integral does not
behave nicely when one studies sequences of functions, such as the
partial sums of a Fourier series approximating a periodic
function. When can one move the limit inside the integral?
In this course we will study the Lebesgue integral, and more
general concepts of integrals and measure. Among other things we will
see how the above problems are resolved and we will study the
important Lp spaces of functions.
The material in this course is fundamental also for the study of
probability theory.
Read more here:
Foundations of Analysis
KTH, SF 2713, Lars Svensson
Course page
Homological Algebra och Algebraic Topology
KTH, SF 2735, Roy Skjelnes/Wojciech Chacholski
Course page
Topology describes continuous and geometric phenomena of
spaces. An effective way to study and analyze these phenomena is
provided with the use of invariants. The idea is to assign to topological
spaces algebraic objects called invariants, which are supposed to capture
certain properties of spaces.
For instance the group of closed paths starting on a given point of the
topological space, called the fundamental group, is such an invariant.
This invariant captures the existence of 1 dimensional holes in the
space. Other important invariants are provided by the singular homology
groups.
The aim of the course is to define these invariants and illustrate their
use with some applications and examples. An important aspect of the course
will be how to learn to calculate such invariants effectively.
The formalism in homological algebra is motivated by the invariant
construction for spaces, stressing the underlying algebraic
structures. The key ingredient is the notion of taking the homology of a
chain complex. The algebraic notion of homology without reference to
topological spaces, plays an important role in modern mathematics.
Homological algebra is a research discipline of its own, but its
principles also play important role in algebraic geometry and
not to mention in algebraic topology. In the course we will focus on the
category of chain maps and modules, where vector spaces and abelian groups
will constitute our main examples. The fundamental concepts of Ext and Tor
will be explained.
Read more here:
Spring 2010
Financial Mathematics, Basic Course
KTH, SF 2701, Harald Lang
Course page
Fourier Analysis
KTH, SF 2705, Håkan Hedenmalm
Course page
Functional Analysis
SU, MM8009 (SF2707), Andrzej Szulkin
Course page
Combinatorics
SU, MMXXXX (SF2708), Petter Brändén
Course page
Combinatorics can be described as the mathematics of discrete, typically finite, objects. The focus of this course is the branch of combinatorics which is branded "enumerative". In essence, this means that we study techniques for counting finite sets. We are interested in questions of the kind "How many gadgets of type G have property P?"
A recurring theme is that enlightening, combinatorial, proofs are to be preferred whenever possible. The guiding philosophy is that the best way to understand why set A and set B have equally many elements is to exhibit a bijection between A and B.
Sometimes combinatorics is considered isolated from the rest of mathematics. Indeed, many of its problems can be stated, and sometimes solved, without reference to any deeper theory. The same is true for some of the applications, for example in computer science or computational biology. In this course, however, we adopt a different point of view, highlighting the connections between combinatorics and other mathematical subjects. As an illustration, the "Möbius function" is a combinatorial device that we associate with any partially ordered set. We introduce it in order to facilitate counting arguments of inclusion-exclusion type. However, if one lifts one's view, the Möbius function can be considered an "Euler characteristic". This connects our counting problems with the world of algebraic topology and gives us access to its wide arsenal of tools.
Read more here:
Selected Topics in Mathematics II: Potential Theory
KTH, SF 2716, Björn Gustafsson
Course page
Potential theory has its physical origin in Newton's and Coulomb's
laws of gravitational and electrostatic attraction. These laws of
distant action invite for concepts of fields which mediate the
action. The fields themselves are vector fields which satisfy rather
involved systems of equations (like Maxwell's equations), but part
of these equations can be automatically resolved by setting the
field up as the gradient a scalar potential field, and then
the remaining part become a quite tractable equation for this
potential, namely Laplace's equation.
Thus classical potential theory studies solutions of Laplace's
equation, namely harmonic functions, and more generally sub-
and superharmonic functions. In the case of two dimensions, the
field equations reduce to essentially the Cauchy-Riemann system, the
solutions of which are the analytic functions. Mathematical
potential theory originated in the work of Green, Gauss and others
in the early 19th century, and has since that time served as a
powerful tool both in treating equations arising in physics and in
the pure mathematical theory of analytic functions.
During the 20th century mathematical potential theory developed
in many directions (e.g., parabolic, probabilistic, abstract and
discrete potential theory, pluripotential theory and various kinds
of nonlinear potential theory). At the same time new kinds of
potentials came up in physics: in Einstein's theory of general
relativity (which has Newton's theory as a limiting case) the role
of potentials is played by the coefficients of the four dimensional
space-time metric, and in gauge field theories, for the fundamental
forces besides gravitation, the role of potentials is taken by
connection coefficients. The famous Aharonov-Bohm effect shows that
in such contexts the potential has a real physical meaning, and is
not just a mathematical tool (as in classical physics).
Two dimensional potential theory is particularly rich because of its
connections to analytic function theory, and the step from two
dimensions to higher dimensions is very easy. Thus the
two-dimensional theory is a suitable starting point.
Read more here:
The History of Mathematics
KTH, SF 2719, Jockum Aniansson
Course page
Representation Theory for Finite and Compact Groups
SU, MM8006,
Course page
Groups and Rings
KTH, SF 2729, Michelle Bucher-Karlsson/Sandra Di Rocco
Course page

As James Newman once said, algebra is "a branch of mathematics in which
one does something to something and then compares the results with the
result of doing the same thing to something else, or something else to
the
same thing".
Abstract algebra is the area of mathematics that investigates algebraic
structures. By defining certain operations on sets one can construct
more
sophisticated objects: groups, rings, fields.
These operations unify and distinguish objects at the same time. Adding
matrices work similarly to adding integers
while matrix multiplication is quite different from multiplication
modulo n.
Because structures like groups or rings are richer than sets we cannot
compare them using just their elements, we have to relate their
operations
as well. For this reason group and ring homomophisms are defined. These
are functions between groups or rings that "respect" their operation.
This type of function are used not only to relate these objects but
also
to build new ones, quotients for example.
Although at this point it may seem like the study of these new and
strange
objects is little more than an exercise in a mathematical fantasy world,
the basic results and ideas of abstract algebra have permeated and are
at
the foundation of nearly every branch of mathematics.
This course is divided in two parts:
- Group Theory
- Rings and Modules
Read more here:
Dynamics of Strings and Membranes
KTH, Jens Hoppe
Room 3733 (KTH), Tuesdays and Thursdays 15-17. Course start: January 12
The course will be an introduction, including M(atrix)-theory,
to the theory of relativistic extended objects (classically:
time-like manifolds that are stationary points of the volume-functional),
and will be given (with different levels of examination) both as a
higher level course (avancerad kurs) for undergraduate students,
and as a graduate course for PhD students.
Literature:
- A First Course in String Theory by B. Zwiebach
(developed at MIT as a (highly praised) string-theory course for
undergraduates).
- Original research articles
|
|