|
Här nedan är Taylorutvecklingen av en R2 ->R - funktion,
dvs. en funktion som geometriskt representeras av en yta i 3-dimensionella rummet,
omkring (x,y) = (xo, yo).
Den linjära delen är märkt rosa.
Endast 0:e och 1:agradstermerna är utskrivna.
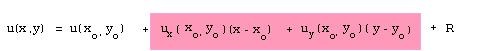
Den linjära och konstanta delen utgör ekvationen för ett plan,
ytans tangentplan i punkten (xo, yo, zo)
där zo = u(xo,yo).
Om man sätter z= u(x,y), zo = u(xo,yo),
A = ux(xo,yo) och
B = uy(xo,yo)
får man tangentplanets ekvation;:
z = zo + A(x - xo) + B(y - yo).
|
Man kan alltså hitta ekvationen för en ytas tangentplan
i den linjära (och konstanta) delen av Taylorutvecklingen
för den funktion som definierar ytan.
Om utvecklingen sker omkring x=xo, y=yo
erhålles tangentplanet i punkten (xo, yo, zo)
där zo = u(xo,yo).
Detta förutsätter att ytan verkligen har ett tangentplan i punkten,
dvs. är differentierbar
Differentierbarhet innebär att resttermen R här till vänster
kan skrivas R = r·b(x,y) , där
r = ( (x-xo)2 + (y-yo)2)1/2 och där
b(x,y) -> 0 då (x,y) -> (0,0).
AM II 6.3
|





