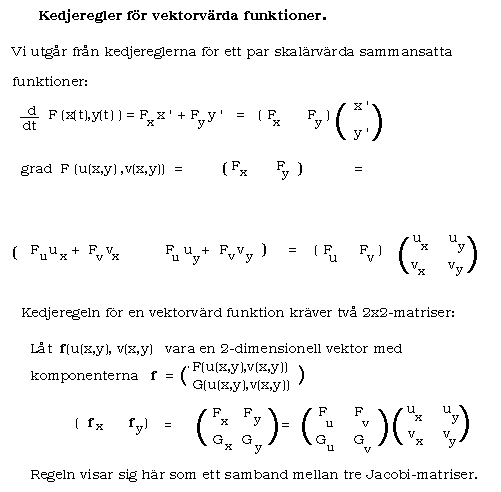
|
Den grundläggande kedjeregeln för flervariabelfunktioner
är:
f'(t) = Fxx'(t) + Fyy'(t) + Fzz'(t)
där f(t) = F(x(t), y(t), z(t) ).
Högerledet här är ju en skalärprodukt mellan grad F och tangentvektorn
( x',y',z' ).
Då den yttre funktionen F är vektorvärd kommer dessa skalärprodukter
att förekomma på flera ställen som komponenter i vektorer eller matriser.
Därmed beskrivs motsvarande kedjeregler bäst av matriser.
Kedjeregeln på matrisform längst ned kan med en alternativ beteckning
skrivas:

MAII 4.5.2 och 4.7.
|
|





