Projektuppgift i Matematik 1 för E och Media 2000.

Inlämnas senast onsdagen den 11/10 till lektionsläraren. Tänkbara inlämningsmedia: Papper, dvs utskrift av Maplesession . Maplefil epostad till läraren. HTML-fil utlagd på nätet. URL-adress till läraren (Notera möjligheten att exportera Maple-filer till HTML) I samtliga fall bör sessionen förses med kommentarer. (Använd 'Insert Text input') Tala med läraren om vilket medium som föredras.

Uppgiften består av två deluppgifter, som var och en löses huvudsakligen med hjälp av matematikprogrammet Maple.

Uppgifternas gemensamma tema är störningsräkning.
Detta innebär att man vid lösningen av en uppgift tar hänsyn till eventuella små förändringar av indata. En sådan förändring kan representeras av en parameter eps (epsilon) som man låter följa med i räkningarna varvid även resultatet kommer att bero av eps.
I vissa enkla fall kan man få slutresultatet som en explicit funktion av eps, men oftast är detta omöjligt.
I stället kan man använda sig av en MacLaurin-utveckling som ger ett lättavläst svar på frågan hur lösningen på problemet beror av variabeln eps. Se också OH5.6.

Dina parametervärden

Gå baklänges i ditt personnummer (inkl. de fyra sista siffrorna) och hämta de tre första siffrorna som är

(1) skilda från 0 och

(2) olika.

Kalla dessa siffror a,b resp. c där a < b < c.

Ex: 491224-4007 ger a = 2 , b = 4 och c = 7.

Med hjälp av dessa personliga parametrar definierar vi nu de funktioner som skall studeras i Delupgifterna 1 och 2:

Deluppgift 1

Här studerar vi polynomet

P(x) = p₄ x⁴ + p₃ x³ + p₂x² + p₁x.

där p₄ = c, p₃ = b(-1)^b, p₂ = a och p₁ = -( 2p₂ + 3p₃ + 4p₄)

samt P_eps(x) som erhålles ur P(x) genom att koefficienten p_j byts ut mot p_j + eps , j = 2, 3 eller 4 enligt regeln:

j = 4 om b = 7 eller 8
j = 3 om b = 5 eller 6
j = 2 om b = 2, 3 eller 4
.

Deluppgift 2

I denna uppgift studerar vi funktionen

p_w(x) = (1 - x/M)^w

M sätts till a+b och w till 1 -(-1)^b a/c.

Ex: Med siffrorna i exemplet ovan fås :
P(x) = 7x⁴ + 4x³ + 2x² - 44x och P_eps(x) = 7x⁴ + 4x³ + (2 + eps) x² - 44x samt
p_w(x) = (1 - x/6)^5/7

Deluppgift 1

a. Polynomet P(x) är konstruerat så att P '(1) = 0,
dvs. P har ett stationärt värde för x = 1. Undersök karaktären hos detta värde (lokalt max, min eller terrasspunkt).

b. Studera nu P_eps(x) och undersök hur det stationära värdet P(1) påverkas av eps.
Närmare bestämt:

(i) MacLaurinutveckla den funktion x(eps), som definieras implicit av ekvationen P_eps' (x) = 0
och som uppfyller x(0) = 1, till och med andragradstermen.

(ii) MacLaurinutveckla till och med andra graden funktionen P_eps( x(eps )).
Sätt alltså in MacLaurinpolynomet för x(eps) i P_eps (x) och MacLaurinutveckla resultatet, som ju visar hur extremvärdet påverkas av eps.

Mapletips De Maplekommandon som behövs finns i den korta handledningen . I b. behövs 'implicitdiff' då ekvationen Peps(x) = 0 skall deriveras. Vid insättning av variabel- och parametervärden används 'eval', som också kan användas vid insättning av funktionsuttryck. Observera hur detta kommando ser ut då fler än en substitution utförs samtidigt. b (i). Här bestäms alltså Taylorpolynomet av derivatorna x'(0) och x''(0). Själva polynomet (av 2:a graden) som sedan sätts in i Peps(x) får man själv bygga upp m.hj.a. dessa derivatavärden. b (ii). Efter insättning av Taylorpolynomet i Peps(x) kan det däremot vara praktiskt att använda kommandot 'taylor' för att MacLaurinutveckla resultatet av insättningen till och med andra graden. Även Maplesession 4 ger stor hjälp här.

Anm: Ekvationen P_eps(x) = 0 är en tredjegradsekvation och kan lösas explicit av Maple med 'solve'.
Dock blir resultatet ganska svåröverskådligt (tre komplicerade rotuttryck varav två med komplexa inslag) varför vi inte rekommenderar den vägen i detta fall.
Implicit derivering tycks vara att föredra.

Deluppgift 2

a. Vi sätter F(x) = x·p_w(x) = x·(1 - x/M)^w
(med dina parametervärden insatta).

Bestäm maximumvärdet av F(x) på intervallet [0,M] genom att lösa ekvationen F'(x) = 0 och sätta in den unika roten x_o i F(x).
( x_o är unik i ]0,M[ ).
Verifiera också att F''(x_o) < 0.

b. Vi undersöker nu på samma sätt funktionen

F_eps(x) = x·((1-eps)·p_w(x) + eps·q(x)),

där q(x) = (1-x²/M²)^1/10. (Med ditt M-värde).

F_eps(x) är en linjärkombination av
x·p_w(x) och x·q(x) som är = p·_w(x) då eps = 0
och = x·q(x) då eps = 1.

F_eps(x) kan därför ses som en störd version av F(x).
Vi kan nu undersöka hur denna störning eps påverkar maxvärdet för F_eps(x) .
Följande skall utföras:

(i) Derivera F_eps(x) med avseende på x.

(ii)MacLaurinutveckla som i Deluppgift 1 den funktion x(eps) som definieras implicit av ekvationen F_eps'(x) = 0 till och med andra graden.
Notera att värdet x(0) här är det x_o-värde som erhölls i a..

(iii) Sätt in det så erhållna andragrads MacLaurinpolynomet i F_eps(x) och MacLaurinutveckla resultatet till och med andra graden.

Mapletips Bestämningen av derivatan xeps'' ger här större problem än i Deluppgift 1. Maple-kommandot 'implicitdiff(Fpeps=0,x,eps,eps); ' klarar normalt inte av denna kalkyl. Man kan istället utgå från derivatan x'(eps) som Maple klarar av och ger som en funktion x'(eps) = H(x,eps). Man kan visa (flervariabelkalkyl ) att x'' = Hx·x' + Heps, där Hx beräknas av kommandot ' diff(H,x); ' och Heps av kommandot 'diff(H,eps); '. Dessutom är ju x' = H(x,eps). Gör sedan som i Deluppgift 2, dvs använd 'eval' och sätt in eps = 0 , x(0) = xo och x'(0) = H(xo,0) för att bestämma x''(0).

Ekonomisk tolkning

(Detta avsnitt innehåller inga nya deluppgifter)

Problemet i Deluppgift 2 kan ges en ekonomisk tolkning:

Man kan anta att funktionen p_w(x) representerar en efterfrågeprofil för en viss vara på så sätt att funktionsvärdet p_w(x) anger hur stor andel av en population som kan tänka sig att köpa varan för priset x.
Den förväntade intäkten vid en öppen försäljning av varan bör därför bli
x N p_w(x) om priset sätts till x (och N är antalet personer i populationen).
Funktionen p_w(x) antar som man kan se värden i intervallet [0,1].)

Här nedan plottas två p_w-kurvor samt funktionen q(x):

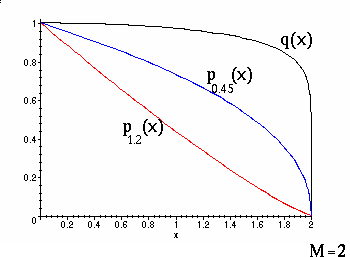
Man ser att avtagande w-värde ger gynnsammare efterfrågeprofil och att q(x) svarar mot en mycket stor efterfrågan även nära maxpriset x=2.

Den störda funktionen F_eps(x) kan tänkas svara mot tänkbara reklamkampanjer av olika styrka (eps-värden) som syftar till att höja efterfrågeprofilen från utgångsläget p_w(x) mot idealtillståndet q(x). Effekten av en sådan kampanj på intäktsfunktionens maximum som funktion av kampanjens styrka (eps-värdet) speglas därför kvantitativt av den erhållna MacLaurinutvecklingen.