Tentan är färdigrättad. Matteinstitutionen har

Hela Listan

på anslagstavlan. Tyvärr gick det unfegär som på övriga linjer, utom I, som läser motvarande kurs: bara 40% godkända. I-linjen hade 72% godkända; nu 76% efter att några tenterat den här tentan. Övriga linjer ligger på mellan 35 och 40%.

Tentorna finns på studentexpeditionen.

Svaren till tentan 1/12   Själva tentan, liksom

Utantill-lista

Tisdag 25/11.

Jag pratade först litet om kon­vergens av generali­serade inte­graler, och an­vände sats 9.14 för att lösa några av upp­gifterna 9.10 i boken. Vi tar alltså inte upp sats 9.15. Jag nämnde kort sats 9.16, och påpekade att om­vändningen inte gäller. Dock tog jag inget exempel på absolut konvergens.

Därefter tog jag upp konver­gensen av MacLaurin­serierna (jag tror Janne också något gjorde det), och visade som exempel hur man kan använda dem för att t.ex. beräkna pi (arctan(1/2)+arctan(1/3)=pi/4) och ln(5) (utveckla ln((1+x)/(1-x)) och sätt x=2/3.)

Sista kvarten härledde jag den enkla varianten av Stirlings formel:

 
och visade som exempel att man nu lätt avgör med rotkriteriet för vilka positiva värden på a som serien

 
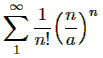
konvergerar. (Den divergerar för a=e; det ser man inte direkt dock.)

Nu återstår bara repetition och upp­hämtning.

Onsdag 19/11.

Jag har blivit uppmärk­sammad på att problem 5 i inlämnings­uppgift 2 är identisk med Ö627f. Ett problem med det kan vara att svaret på den upp­giften i övnings­boken är fel! Om ni får samma svar som övnings­boken, har ni alltså räknat fel!

Tisdag 18/11.

Jag hade hosta och kände mig dålig, men föreläste ändå -- sedan åkte jag hem.

Jag hann inte riktigt med det jag förespeglade. Jag tog upp följande:

1. Rotationsvolym. Jag definierade V(x) som den volymen fram till x-värdet x, och visade att V'(x)=A(x) = tvärsnittsarean (generellt; inte bara för rotationsvolym.) Så volymen V=V(b)-V(a) = integralen från a till b av A(x) [a och b är ändpunkterna i x-led för volymen.] Beräknar volymen av ett klot.

2. Parametriserade kurvor. Exempel: cykloiden. Jag härdedde uttrycket för båglängd (dvs. derivatan av båglängden, som jag sedan integrerar,) och beräknade cykloidens längd.

3. Jag hann dock inte att ta upp exemplet med volymen av cykloiden då den roterar kring x-axeln (Jmf. Ö751.) vilket jag hade planerat. Nu får lektionslärarna förklara uppgift Ö751 (fast de hinner inte läsa det här före lektonen.)

4. Area av sektor: 2A'(t) = x(t)*y'(t)-y(t)*x'(t). Som specielfall polära koodinater: 2A'(t)=r^2(t). Den första formeln ingår inte formellt i kursen, men den är inte svårare än specialfallet polära koordinater. Jag tog exempel på bägge formlerna.

Någon tid för annat blev det inte.

Torsdag 13/11

Jag tog inte upp något om medel­värden för inte­graler -- om lektions­lärarna vill kan de ta upp det något på lektio­nerna, men det är ett perifert inslag i kursen.

Jag pratade om generali­­serade inte­­graler, och på­pekade att fundamental­satsen att inte­­gralen från a till b av f(x) är F(b)-F(a) om

1. F(x) är konti­nu­erlig i hela inter­­vallet [a,b], och

2. F '(x) = f(x) utom eventu­ellt i ändligt många punkter.
 
gäller även om f(x) är obe­gränsad. Exempel:

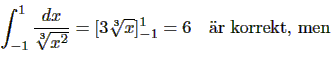
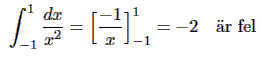
Vi beräk­nade också inte­gralen

 
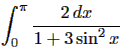
på diverse olika sätt ("primitiven" arctan[2*tan(x)] får ett språng i x=pi/2), se bokens exempel 7.3.3 som är snar­likt.

Jag tog också upp inde­graler över obe­gränsat inter­vall, och in­förde konver­gent" och "diver­gent" inte­gral.

Slutligen tog jag upp något om substitu­tion med sin och sinh då inte­granden har rot­uttryck, men det gick ganska snabbt, så jag vet inte om det gick hem riktigt.

Tisdag 11/11

Nu finns inlämnings­uppgift 2. Lämnas till lektions­läraren senast 21/11.

Idag gick jag igenom upp­delning i partial­bråk. Jag tog också upp substitu­tionen t=tan(x/2) för trigono­metriska inte­grander och tog ett enkelt exempel på detta. Jag antydde också att om man har ett uttryck med tan(x), sin(x)*cos(x) och jämna potenser av sin(x) och cos(x), så går det bra med substitu­tionen t=tan(x). Jag bestämde också primi­tiverna till sin²(x) och cos²(x); se "utantill-listan" ovan. Inte­gralerna där tycker jag man kan ta som givna. Mer hann jag inte. Jag tog alltså inte upp rot-uttryck.

Torsdag 6/11

Jan Kristoferson föreläste, eftersom jag var på hel­dagssemi­narium med fakultets­kollegiet. Han gick igenom inte­graler, per kurs­planering, men hann inte med partiell inte­gration. Det tas upp på lektionen i morgon.

Tisdag 4/11

Jag gick igenom partikulär­lösningar till andra ordningens in­homogena diff.­ekva­tioner y"(x) + ...= f(x). Jag gjorde samma saker jag gjorde för I, dvs. jag tog upp upp

1)   f(x) = polynom. Ansätt polynom av samma grad (såvida inte resonans; se nedan.)

2)   f(x) = e^ax g(x). Ansätt y(x) = e^ax v(x) och sätt in i diff.­ekva­tionen. Efter att vi divi­derat bort e^ax åter­står en diff.­ekvation i v(x): v"(x) + ... = g(x) som vi får försöka lösa. Jag på­pekade "för­skjutnings­regeln" som kan formu­leras så att karak­teris­tiska polynomet för ekva­tionen som hör till v(x) är 1/2 p"(a) t² + p'(a)t + p(a), där p(t) är karak­teris­tiska polynomet till ur­sprung­liga diff.­ekva­tionen. Man kan redu­cera räkning­arna något genom att använda för­skjutnings­regeln, men det är bättre att deri­vera e^ax v(x) och sätta in, om man är minsta osäker på metoden.

3)   f(x) = a sin(wx) + b cos(wx). Ansätt y(x)= A sin(wx) + B cos(wx), såvida inte resonans; se nedan.

4)   Resonans. Jag tog upp två fall: Om A sin(wx) + B cos(wx) är lösning till den homo­gena ekva­tionen, går det inte att an­sätta detta som partiku­lär­lösning i 3) ovan. Man får då an­sätta Ax sin(wx) + Bx cos(wx) i stället. Fall två: om f(x) är polynom, och konstant­termen i diff.­ekvationen är noll, så är ju alla kon­stanter lösningar till homogena ekva­tionen. Man får då an­sätta y(x)=polynom av ett snäpp högre grad, med kon­stant­term = 0.

Jag räknade igenom följande exempel, och använde ovan­stående metoder: y"(x) + 4 y'(x) + 13 y(x) = f(x), där

1)   f(x) = x².

2)   f(x) = x² e^-2x. Med metod 2) och sedan 1) ovan.

3)   f(x) = sin(x). Med metod 3) ovan.

4)   e^-2x sin(3x). Med metod 2) ovan. Vi får då en ekva­tion för v(x): v"(x) + 9 v(x) = sin(3x). Detta ger reso­nans: metod 4 ovan.

5)   Ett annat höger­led: y"(x) + y'(x) - 2 y(x) = x e^-2x. Efter an­sätt­ning enligt metod 2) ovan får vi v"(x) - 3 v'(x) = x. Detta ger reso­nans, så vi an­sätter v(x) = ax² + bx.

Anmärkning Observera: Jag an­vänder alltså inte komplexa exponen­tial­funktioner i exemplen 3) och 4) ovan. Jag nämnde inte den möjlig­heten; jag tror inte det är någon väsentlig för­enkling, och risken för fel ökar, miss­tänker jag. Men såvitt jag förstår har studenterna läst komplexa tal i den andra mattekursen som började tidigare, så det är givet­vis fritt fram för lektionsl­ärarna att an­vända komplexa expo­nential­funktionen, om de tycker det och stu­denterna är med på noterna.

Torsdag 30/10

Första timmen fortsatte jag med Taylor­utvecklingar. Bl.a. här­ledde jag ut­veckling­arna för ln(1+x+x²) genom att använda den kända utveck­lingen för ln(1+x), och utveck­lingen av sin(x) kring x=pi/4 genom att skriva sin(t+pi/4)=1/rot(2)*(cos t + sin t) och an­vända kända utveck­lingar för sinus och cosinus.

Andra timmen gick jag igenom lösningen till homogena differential­ekvationer av andra ordningen med konstanta koeffici­enter.

Tisdag 28/10

Jag gick igenom Taylors formel, med Lagranges rest­term. Men jag ut­vecklar bara kring x=0; jag före­drar att införa en variabel t = x-a och ut­veckla kring t=0 i stället för att ut­veckla kring x=a. (Det är dess­utom enklare att ut­veckla t.ex. sin(t+a) = cos(a)*sin(t) + sin(a)*cos(t) kring t=0 med kända ut­vecklingar än att ut­veckla sin(x) kring x=a.)

I allmän­het skriver jag rest­termen som xⁿ⁺¹H(x) där H(x) har ett gränsv­ärde så x-->0. Jag tror det är peda­gogiskt dumt att omedel­bart införa Ordo-beteck­ningen -- det gör nog saken svårare i stället för enklare. Jag tror vi skall åt­minstone i början skriva på "mitt" sätt -- när man vant sig kan det vara dags för Ordo.

Taylor­utveckling­arna för 1/(1-x), ln(1+x), arctan(x), e^x, sin(x), cos(x) och (1+x)^a är utantill-kunskaper. Jag tog upp entydig­heten för Taylor som sats, men jag gjorde inget bevis för den -- det kan intress­erade läsa i boken.

Jag tog också upp L'Hôpitals regel, även då täljare och nämnare går mot oändlig­heten, och tog ett par enkla exempel. Däremot hann jag inte med något bevis -- det kan vi ta nästa gång.

Torsdag 23/10

Första timmen var helt teoretisk. Jag på­pekade den logiska gången: exis­tens av extrem­punkter --> deri­vatan = 0 i extrem­punkt --> Rolles lemma --> medel­värdes­satsen och Cauchys medel­värdes­sats. Jag be­visade dessa satser, utom den första. Cauchys medel­värdes­sats kommer vi att an­vända för att här­leda Tayloru­tveckling och för L'Hôpitals regel.

Andra timmen löste jag problem, nämligen upp­gifterna 4.20 och 4.24 i boken.

Tisdag 21/10

Jag formulerade differential­kalkylens medel­värdes­sats, men gav inget bevis (kommer senare) och använde den för att visa att derivatan >0 ==> växande, respektive derivatan <0 ==> avtagande. Sedan pratade jag om andra­derivatans tecken: konvexa och konkava funktioner. Jag visade att konvex (dvs. f "(x)>0) medför att grafen ligger under sin korda och över sin tangent, och mot­svarande, mutatis mutandis, för konkava funktioner. Jag tog ett par exempel på detta. Vi analyserde också ett tredje­grads­ploynom med avseende på växande / avtagande och konvex / konkav i en "teckentabell" (ungefär som på sidan 147 i kursboken.)

Andra timmen talade jag om kurvors på formen y=f(x) krökning, och här­ledde kröknings­formeln för sådana. Jag fick då till att börja med härleda uttrycket för båg­längdens derivata m.a.p. x. Vi hann inte beräkna krökningen för en cirkel, så jag gav som övning att visa att den är 1/radien. Men vi såg att krökningen för y=x² är störst för x=0 och mycket liten för stora x, i överens­stämmelse med vad vi ser i en figur..

Syftet med hela före­läsningen idag var dels att ge litet intuitiv och geo­metrisk tolkning av derivatans och andra­derivatans tecken; dels att ge exempel på model­lering där derivator av första och andra ordningen utnyttjas.

Torsdag 16/10

Jag följde kurs­planeringen. Gick igenom deri­verings­reglerna, även kedje­regeln i tapp­ningen "deri­vera m.a.p. ett x i taget och addera." Vi deri­verade på det viset x^x genom att deri­vera x^a och a^x m.a.p. x och addera med a=x. Detta är som för­beredelse till sättet att tänka när man an­vänder kedje­regeln i flera variabler.

Jag tog också upp "loga­ritmisk deri­vering" med några exempel, och implicit deri­vering i största allmän­het. Vi här­ledde deri­vatorna av de cyklo­metriska funk­tionerna genom att deri­vera sin(y(x)) = x implicit, osv. Jag tycker generellt det är enklare att beräkna in­versers deri­vator genom att derivera implicit på detta sätt, i stället för att an­vända en speci­fik formel för det.

Slut­ligen visade jag att deriver­bara funk­tioner är kontinu­erliga, och bevisade formeln för deri­vatan av en produkt. Jag fick frågan om det gällde tvärt om: är alla kontinu­erliga funk­tioner deri­verbara, och svarade att nej, det finns t.o.m. kontinu­erliga funk­tioner som inte är deriver­bara för något enda x.

Tisdag 14/10

Ursäkta -- det här kommer inte förrän sent på kvällen. Men jag följde kurs­planderingen: jag defini­erade konti­nuitet, och bevisade som exempel att sin(x) är kontinu­erlig. Sedan formu­lerade jag "satsen om mellan­liggande värden". Som exempel tog jag en variant av övning 3.2 i Eikes bok -- vi visade ordent­ligt att den rele­vanta funk­tionen verkligen är kontinu­erlig!

Andra timmen formu­lerade jag "satsen om extrem­värden" (existens av största och minsta värde). Jag visade med några exempel vad som kan gå fel om förut­sättning­arna inte är uppfyllda.

Därefter började vi med deri­vator. Jag defini­erade derivata, och beräk­nade ur defini­tionen deri­vatan av sin(x) och xⁿ. Jag skrev också upp en utantill-lista på deri­vatan av de elemen­tära funktio­nerna -- även de cyklo­metriska, trots att vi ännu inte härlett dem och de inte heller är kända från gymnasiet.

Torsdag 9/10

Jag gick igenom gränsvärden, och gav även epsilon-delta definitionen. Däremot bevisade vi inga satser, men jag visade med utgångspunkt från definitionen att limes av roten ut x då x-->pi är roten ur pi. Vi såg att som delta kunde man ta roten_ur(pi)*epsilon, eller varför inte helt enkelt delta = epsilon.

Sedan visade jag ett par gränsvärden med instängning: sin(x)/x då x-->0, och ln(x)/x^a då x-->oändl. och a>0, bl.a. Jag tog också en rationell funktion, med täljare och nämnare av samma grad (3) och x-->oändl.

Jag tog aldrig något exempel då gränsvärdet är oändligt -- det är bra om lektionslärarna gör det och säger något om innebörden -- jag tog alltså inte upp det ö.h.t. (däremot då x-->oändl.)

En viss förvirring hos några väckte exemplet n-te.roten_ur n, då n-->oändl. Man vill gärna låta först ena n:et och sedan det andra gå mot oändligheten. Jag diskuterade detta genom exemplet (2x+y)/(x+y) och tog limes först då x-->0 och sedan y-->0, och därefter tvärtom. Men jag tror inte poängen gick fram till hundra procent. Vi kommer ju så småningom till exempel som (1+x/n)ⁿ då n-->oändl., så vi kommer tillbaks till fenomenet, men om lektionslärarna vill ta upp det här och belysa det ytterligare är det värdefullt!

Det här avsnittet är ganska svårt, och jag påpekade att vi skall skaffa verktyg för att beräkna gränsvärden senare i kursen (L'Hospital och Taylor), så en del exempel som nu verkar tekniskt svåra kommer vi att kunna behandla betydligt enklare senare.

Tisdag 7/10

Kommentarer till lärarna.

Jag pratade litet om inversa funktioner i allmänhet, och gick sedan igenom definitionerna av arcsin, arccos och arctan. Därefter räknade jag några exempel; dels de två från Eikes bok (se länken ovan), dels en uppgift från en gammal tenta.

Observera att det finns flera (ganska lätta) uppgifter på detta i "dagens"; se kursplaneringen.

Torsdag 2/10

Schemaändring: Från och med nästa vecka har vi lektioner klockan 8-10 på onsdagarna, och övningar 13-15 i stället för tvärtom.

Jag pratade binomial­koeffici­enter hela före­läsningen. Vi tar talen i Pascals triangel som definition av binomial­koeffici­enter, sedan visade jag med induktion tolkningen att är antalet sätt att plocka ut k element bland n och likaså med induktion formeln för binomial­koeffici­enten uttryckt i fakul­teter. Jag skrev upp binomial­satsen (a+b)ⁿ = ...och moti­verade den kombina­toriskt.

Vi räknade ut sanno­likheten att man får fyra ess i en bridge­hand. Så här­ledde jag, efter en del strulande, formeln

och använde den för att här­leda ett uttryck för summorna 1 + 2 + ... + n och 1² + 2² + ... + n². Detta är ju en god hjälp till uppgift två på in­lämnings­uppgifterna, så jag hoppas ni börjar göra dem nu.

Tisdag 30/9

Jag tog några exempel på inuktionsbevis. Därefter pratade jag om summasymbolen, och visade hur man kan skifta index i en summa. Jag använde setta för att beräkna några summor genom att skriva om dem som teleskoperande serier, tex.

Slutligen tog jag upp litet om binomialkoefficienter och Pascals triangel.

Här är några övningar på summasymbolen, lämpliga att titta på på övningen i morgon. Jag föreslår att ni också tittar på "Dagens 1", uppgifterna till dag 26/8 (induktionsbevis) på sidan för kursplanering på den övningen.

Här är första om­gången av inlämnings­uppgifter. Börja redan nu att arbeta med dem, men vi bestämmer senare datun för när de skall lämnas in. Reglerna är: Ni får sam­arbeta, och det är OK att fråga lärare eller andra om detaljer. Men det är inte tillåtet att skriva av någon annans lösningar. Var och en skall alltså stå för sina egna lösningar, och vara beredd att redogöra för dem. Från oss lärares sida är syftet med inlämnings­uppgifterna att ni skall lära er matematiken, inte i första hand att det skall under­lätta tentamen.